ACCUPLACER AAF Test Prep
If you are serious about getting a great score on your Accuplacer AAF test, try out our recommended Accuplacer AAF Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Which of the following is equivalent to $x^3 − 5x^2 − 26x + 120$?
$(x + 4)(x^2 − 6x + 30)$ | |
$(x + 3)(x^2 − 8x + 40)$ | |
$(x + 6)(x^2 − 4x + 20)$ | |
$(x + 5)(x^2 − 10x + 24)$ |
Question 1 Explanation:
The correct answer is (D). There are two general approaches that might be used to solve this problem:
1) synthetic division
2) work backwards from the possible answers
Since synthetic division is probably quicker and also worth reviewing, we will use this approach.
Check to see if $(x + 4)$ is a factor:
$\begin{array}{c|rrrr}-4&1&-5&-26&120\\&↓&-4&36&-40\\\hline\ & 1 & -9 & 10 & 80\\\end{array}$
The remainder is $80$ so $(x + 4)$ is not a factor of $x^3 − 5x^2 − 26x + 120$.
Check to see if $(x + 5)$ is a factor:
$\begin{array}{c|rrrr}-5&1&-5&-26&120\\&↓&-5&50&-120\\\hline\ & 1 & -10 & 24 & 0\\\end{array}$
The remainder is $0$ (zero) and the quotient is $1x^2 − 10x + 24$.
Therefore, $(x + 5)(x^2 − 10x + 24)$ is equivalent to $x^3 − 5x^2 − 26x + 120$.
1) synthetic division
2) work backwards from the possible answers
Since synthetic division is probably quicker and also worth reviewing, we will use this approach.
Check to see if $(x + 4)$ is a factor:
$\begin{array}{c|rrrr}-4&1&-5&-26&120\\&↓&-4&36&-40\\\hline\ & 1 & -9 & 10 & 80\\\end{array}$
The remainder is $80$ so $(x + 4)$ is not a factor of $x^3 − 5x^2 − 26x + 120$.
Check to see if $(x + 5)$ is a factor:
$\begin{array}{c|rrrr}-5&1&-5&-26&120\\&↓&-5&50&-120\\\hline\ & 1 & -10 & 24 & 0\\\end{array}$
The remainder is $0$ (zero) and the quotient is $1x^2 − 10x + 24$.
Therefore, $(x + 5)(x^2 − 10x + 24)$ is equivalent to $x^3 − 5x^2 − 26x + 120$.
Question 2 |
If $f(x) = (x −3)(x + 3)$, what is $f(x + 3)$?
$x^2 − 18$ | |
$x^2 − 6x$ | |
$x^2 − 9$ | |
$x^2 + 6x$ |
Question 2 Explanation:
The correct answer is (D). To find $f(x + 3)$, we must substitute $(x + 3)$ everywhere we have an $x$ in the original equation.
$f(x) = (x − 3)(x + 3)$
$f(x + 3)$ $ = ((x + 3) − 3)((x + 3) + 3)$
$= (x + 3 − 3)(x + 3 + 3)$
$= (x)(x + 6)$
$= x^2 + 6x$
$f(x) = (x − 3)(x + 3)$
$f(x + 3)$ $ = ((x + 3) − 3)((x + 3) + 3)$
$= (x + 3 − 3)(x + 3 + 3)$
$= (x)(x + 6)$
$= x^2 + 6x$
Question 3 |
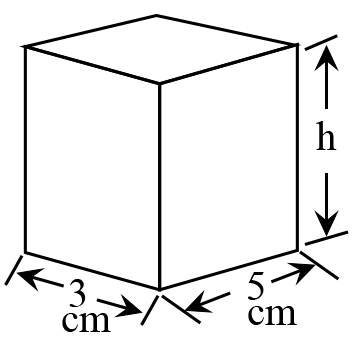
The right rectangular prism shown has a surface area of 142 cm2. What is the height, $h$, of the prism? Recall that the surface area of this prism can be found by finding the sum of the areas of each of the rectangular faces, and the area of a rectangle is its length times its width.
$5$ | |
$7$ | |
$6$ | |
$8$ |
Question 3 Explanation:
The correct answer is (B). The right rectangular prism shown has three pairs of rectangular faces. We need to find the area of each of these pairs of faces.
Area of pair 1: $(3)(5) + (3)(5) = 30 \text{ cm}^2$
Area of pair 2: $(3)(h) + (3)(h) = 6h \text{ cm}^2$
Area of pair 3: $(5)(h) + (5)(h) = 10h \text{ cm}^2$
Surface area $= 30 + 6h + 10h$
$= 30 + 16h$
Since the surface area was given as $142 \text{ cm}^2$ we have:
$142 = 30 + 16h$
$112 = 16h$
$\dfrac{112}{16} = h$
$h = \dfrac{112}{16} = \dfrac{56}{8} = \dfrac{7}{1}$
$h = 7 \text{ cm}$
Area of pair 1: $(3)(5) + (3)(5) = 30 \text{ cm}^2$
Area of pair 2: $(3)(h) + (3)(h) = 6h \text{ cm}^2$
Area of pair 3: $(5)(h) + (5)(h) = 10h \text{ cm}^2$
Surface area $= 30 + 6h + 10h$
$= 30 + 16h$
Since the surface area was given as $142 \text{ cm}^2$ we have:
$142 = 30 + 16h$
$112 = 16h$
$\dfrac{112}{16} = h$
$h = \dfrac{112}{16} = \dfrac{56}{8} = \dfrac{7}{1}$
$h = 7 \text{ cm}$
Question 4 |
$f(x) = (3 − x)(x + 3)$. What is the value of $f(−5)$?
$−16$ | |
$4$ | |
$−4$ | |
$64$ |
Question 4 Explanation:
The correct answer is (A). To find $f(−5)$, we need to plug in $−5$ everywhere we see $x$ in the original expression:
$f(−5) = (3 − −5)(−5 + 3)$
$= (3 + 5)(−5 + 3)$
$= (8)(−2)$
$= −16$
$f(−5) = (3 − −5)(−5 + 3)$
$= (3 + 5)(−5 + 3)$
$= (8)(−2)$
$= −16$
Question 5 |
$x + 2 = x^2 − 2x − 8$
What value of $x$ satisfies this equation?$2$ | |
$−3$ | |
$−\dfrac{4}{3}$ | |
$5$ |
Question 5 Explanation:
The correct answer is (D). When solving quadratics (equations with an $x^2$ term), typically it is best to get everything on one side of the equation:
$x + 2 = x^2 − 2x − 8$
$0 = x^2 − 2x − 8 − x − 2$
Simplify:
$0 = x^2 − 3x − 10$
factor:
$0 = (x − 5)(x + 2)$
$x = 5$ and $x = −2$ are both solutions.
Note: you could also solve this problem by plugging each answer into the original equation and seeing which of the answers provides a correct result:
$x + 2 = x^2 − 2x − 8$
Try $x = 5$
$5 + 2 = 5^2 − 2(5) − 8$
$7 = 25 − 10 − 8$
$7 = 7$ is true.
$x + 2 = x^2 − 2x − 8$
$0 = x^2 − 2x − 8 − x − 2$
Simplify:
$0 = x^2 − 3x − 10$
factor:
$0 = (x − 5)(x + 2)$
$x = 5$ and $x = −2$ are both solutions.
Note: you could also solve this problem by plugging each answer into the original equation and seeing which of the answers provides a correct result:
$x + 2 = x^2 − 2x − 8$
Try $x = 5$
$5 + 2 = 5^2 − 2(5) − 8$
$7 = 25 − 10 − 8$
$7 = 7$ is true.
Question 6 |
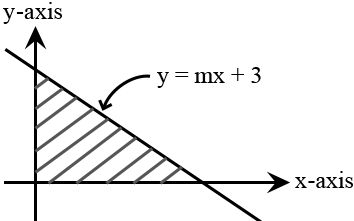
A triangular region is formed by the $x$-axis, $y$-axis, and the line $y = mx + 3$.
What value of $m$ will result in the bounded (shaded) region having an area of 12 units2? The area of a triangle is $\frac{1}{2} \cdot \text{base} \cdot \text{height}$.$−\dfrac{3}{8}$ | |
$−\dfrac{1}{2}$ | |
$−\dfrac{5}{8}$ | |
$−\dfrac{1}{4}$ |
Question 6 Explanation:
The correct answer is (A). The line $y = mx + 3$ has a $y$-intercept of $3$.
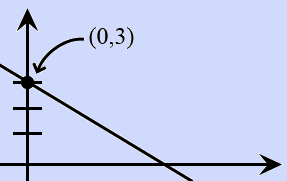
This means our triangle has a height of $3$:
We know the area is $12 \text{ units}^2$:
$\dfrac{1}{2} \cdot 3 \cdot \text{base} = 12$
$3 \cdot \text{base} = 24$
base $= 8$
Our triangle has a base $= 8$.
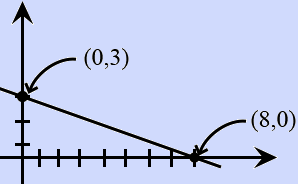
The line goes "down $3$ and over $8$," so the slope is $−\dfrac{3}{8}$.

This means our triangle has a height of $3$:

We know the area is $12 \text{ units}^2$:
$\dfrac{1}{2} \cdot 3 \cdot \text{base} = 12$
$3 \cdot \text{base} = 24$
base $= 8$
Our triangle has a base $= 8$.

The line goes "down $3$ and over $8$," so the slope is $−\dfrac{3}{8}$.
Question 7 |
What is the maximum $y$ value reached by the function $f(x) = −x^2 + 10x − 21$?
$6$ | |
$10$ | |
$8$ | |
$4$ |
Question 7 Explanation:
The correct answer is (D). The maximum (or minimum) of a parabola will always occur at the $x$ value that is halfway between the real roots ($x$-intercepts) of the function.
To find these real roots we need to factor the equation:
$f(x) = −1(x^2 − 10x + 21)$
$f(x) = −1(x − 3)(x − 7)$
The real roots occur at $x = 3$ and $x = 7$.
The $x$ value halfway between $3$ and $7$ is $x = 5$.
When $x = 5$, $f(5) = −(5)^2 + 10(5) − 21 = 4$.
The maximum $y$ value is $y = 4$.
To find these real roots we need to factor the equation:
$f(x) = −1(x^2 − 10x + 21)$
$f(x) = −1(x − 3)(x − 7)$
The real roots occur at $x = 3$ and $x = 7$.
The $x$ value halfway between $3$ and $7$ is $x = 5$.
When $x = 5$, $f(5) = −(5)^2 + 10(5) − 21 = 4$.
The maximum $y$ value is $y = 4$.
Question 8 |
$2^{6x} = 8^6$
What value of $x$ satisfies this equation?$2$ | |
$3$ | |
$4$ | |
$5$ |
Question 8 Explanation:
The correct answer is (B). To solve the equation, we need to rewrite it using an equivalent base.
$8 = 2^3$
Substituting we have:
$2^{6x} = (2^3)^6$
According to rules of exponents:
$2^{6x} = 2^{3 \cdot 6}$
$2^{6x} = 2^{18}$
Since the bases are the same, we can set the exponents equal to each other and solve:
$6x = 18$
$x = 3$
$8 = 2^3$
Substituting we have:
$2^{6x} = (2^3)^6$
According to rules of exponents:
$2^{6x} = 2^{3 \cdot 6}$
$2^{6x} = 2^{18}$
Since the bases are the same, we can set the exponents equal to each other and solve:
$6x = 18$
$x = 3$
Question 9 |
$12 − \sqrt{3x} = 8$
Solve for $x$.$\sqrt{20}$ | |
$4$ | |
$\dfrac{16}{3}$ | |
$\dfrac{4}{3}$ |
Question 9 Explanation:
The correct answer is (C). Begin by isolating the radical ("get the square root part by itself"):
$12 − \sqrt{3x} = 8$
$12 − 8 = \sqrt{3x}$
$4 = \sqrt{3x}$
To get rid of the square root, we need to square both sides:
$(4)^2 = (\sqrt{3x})^2$
$16 = 3x$
$x = \dfrac{16}{3}$
$12 − \sqrt{3x} = 8$
$12 − 8 = \sqrt{3x}$
$4 = \sqrt{3x}$
To get rid of the square root, we need to square both sides:
$(4)^2 = (\sqrt{3x})^2$
$16 = 3x$
$x = \dfrac{16}{3}$
Question 10 |
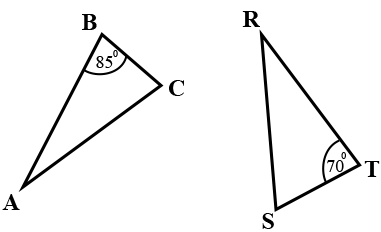
Triangle $ABC$ is congruent to triangle $RST$. What is the measure of angle $R$?
$25$ | |
$40$ | |
$10$ | |
$20$ |
Question 10 Explanation:
The correct answer is (A). We are told that triangle $ABC$ is congruent to triangle $RST$. We know that congruent parts of congruent triangles are congruent (CPCTC).
This means $∠A ≅ ∠R, ∠B ≅ ∠S, ∠C ≅ ∠T$.
Since $∠B$ measure $85°$, we know $∠S$ must also measure $85°$ (m$∠S = 85°$).
It is given that $∠T$ measures $70°$ (m$∠T = 70°$).
The interior angles of a triangle must sum to $180°$:
m$∠R + \text{m}∠S + \text{m}∠T = 180°$
m$∠R + 85° + 70° = 180°$
m$∠R + 155° = 180°$
m$∠R = 25°$
This means $∠A ≅ ∠R, ∠B ≅ ∠S, ∠C ≅ ∠T$.
Since $∠B$ measure $85°$, we know $∠S$ must also measure $85°$ (m$∠S = 85°$).
It is given that $∠T$ measures $70°$ (m$∠T = 70°$).
The interior angles of a triangle must sum to $180°$:
m$∠R + \text{m}∠S + \text{m}∠T = 180°$
m$∠R + 85° + 70° = 180°$
m$∠R + 155° = 180°$
m$∠R = 25°$
Question 11 |
A right triangle has a leg of length $3$, a second leg of length $3x − 5$, and a hypotenuse of length $5$. What is the value of $x$?
$4$ | |
$2$ | |
$3$ | |
$5$ |
Question 11 Explanation:
The correct answer is (C). The Pythagorean theorem states that $a^2 + b^2 = c^2$, where $a$ and $b$ represent the lengths of the legs of a right triangle and $c$ represents the hypotenuse.
For our triangle, the lengths of the legs are $3$ and $3x − 5$. The length of the hypotenuse is $5$.
$a^2 + b^2 = c^2$
$3^2 + b^2 = 5^2$
$9 + b^2 = 25$
$b^2 = 16$
$b = 4$ (the length must be positive)
The length of the second leg is $4$, but we also know it is $3x − 5$.
Setting these equal yields:
$3x − 5 = 4$
$3x = 9$
$x = 3$
For our triangle, the lengths of the legs are $3$ and $3x − 5$. The length of the hypotenuse is $5$.
$a^2 + b^2 = c^2$
$3^2 + b^2 = 5^2$
$9 + b^2 = 25$
$b^2 = 16$
$b = 4$ (the length must be positive)
The length of the second leg is $4$, but we also know it is $3x − 5$.
Setting these equal yields:
$3x − 5 = 4$
$3x = 9$
$x = 3$
Question 12 |
$\log_b64 = 3$
What value of $b$ (the base of the log) satisfies the equation?$10$ | |
$4$ | |
$2$ | |
$8$ |
Question 12 Explanation:
The correct answer is (B). Begin by rewriting the logarithmic equation in exponential form:
$\log_b64 = 3 → b^3 = 64$
To solve we need to determine what number when cubed will give us $64$.
Since $4^3 = 4 \cdot 4 \cdot 4 = 64$, $b$ must be $4$.
$\log_b64 = 3 → b^3 = 64$
To solve we need to determine what number when cubed will give us $64$.
Since $4^3 = 4 \cdot 4 \cdot 4 = 64$, $b$ must be $4$.
Question 13 |
If $f(x) = 4x^2$ and $g(x) = 5x$, what is $g(f(2x))$?
$100x^2$ | |
$80x^2$ | |
$20x^2$ | |
$10x^2$ |
Question 13 Explanation:
The correct answer is (B). First evaluate the inner function by substituting $2x$ into the expression for $f(x)$:
$f(2x) = 4(2x)^2$
$f(2x) = 4(4x^2)$
$f(2x) = 16x^2$
Next substitute the expression for $f(2x)$ into the expression for $g(x)$:
$g(f(2x)) = g(16x^2) \quad$ $\text{(Read as “g of } 16x^2”)$
$g(f(2x)) = 5(16x^2)$
$g(f(2x)) = 80x^2$
$f(2x) = 4(2x)^2$
$f(2x) = 4(4x^2)$
$f(2x) = 16x^2$
Next substitute the expression for $f(2x)$ into the expression for $g(x)$:
$g(f(2x)) = g(16x^2) \quad$ $\text{(Read as “g of } 16x^2”)$
$g(f(2x)) = 5(16x^2)$
$g(f(2x)) = 80x^2$
Question 14 |
$6y(3y − 2) + (3y − 2) =$
$2(3y + 2) − (6y)$ | |
$(3y + 2)(6y − 1)$ | |
$(3y − 2)(6y + 1)$ | |
$(6y − 1)(3y − 2)$ |
Question 14 Explanation:
The correct answer is (C). Consider the form of the answer choices before evaluating the problem. Notice that $(3y − 2)$ is common to both terms, meaning it can be factored out. After factoring out the $(3y − 2)$, only the terms $6y + 1$ remain:
$(3y − 2)(6y + 1)$
If you are struggling to understand, think about how we would factor the similar expression:
$6yx + x$
Since both terms have an $x$ we can factor out an $x$:
$x(6y + 1)$
The only difference between this simpler example and the original problem is that in place of $x$ we have $(3y − 2)$.
$(3y − 2)(6y + 1)$
If you are struggling to understand, think about how we would factor the similar expression:
$6yx + x$
Since both terms have an $x$ we can factor out an $x$:
$x(6y + 1)$
The only difference between this simpler example and the original problem is that in place of $x$ we have $(3y − 2)$.
Question 15 |
A line in the coordinate plane has the equation $5a + b = 7$, where $a$ represents the independent variable, and $b$ represents the dependent variable. Which of the following is the equation of a line that is perpendicular to $5a + b = 7$?
$b = 5a + 3$ | |
$b = -5a - 5$ | |
$b = \left(\frac{1}{5}\right)a - 2$ | |
$b = \left(-\frac{1}{5}\right)a + 1$ |
Question 15 Explanation:
The correct answer is (C). The independent variable is conventionally written as $x$, and the dependent variable as $y$, so we can rewrite the equation into a more familiar form:
$5a + b = 7$
$→ 5x + y = 7$
$→ y = −5x + 7$
Recall that perpendicular lines have slopes that are negative reciprocals of each other. The slope in the given line is $m = −5$. The negative reciprocal is: $\frac{1}{5}$. Only answer choice (C) has a slope of $m =\frac{1}{5}$.
$5a + b = 7$
$→ 5x + y = 7$
$→ y = −5x + 7$
Recall that perpendicular lines have slopes that are negative reciprocals of each other. The slope in the given line is $m = −5$. The negative reciprocal is: $\frac{1}{5}$. Only answer choice (C) has a slope of $m =\frac{1}{5}$.
Question 16 |
In the coordinate plane, point $Z$ lies on the positive $y$-axis and point $Q$ has a $y$-coordinate of $0$ and is five units away from the origin, $O$. The area of triangle $OZQ$ is $12$, what is the $y$-coordinate of point $Z$?
$3.0$ | |
$4.2$ | |
$4.4$ | |
$4.8$ |
Question 16 Explanation:
The correct answer is (D). The best way to approach a geometry word problem such as this is to draw a figure to represent the situation:
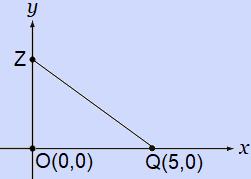
In this case, the easiest way to solve is using the formula for the area of a triangle where $b$ represents the $x$-coordinate of point $Q$, and the variable $h$ represents the $y$-coordinate of $z$:
$\text{Area} = \frac{1}{2}bh$
$12 = \frac{1}{2}5h$
Multiply both sides by 2:
$24 = 5h$
Divide both sides by 5:
$h = \dfrac{24}{5}$
Use long division to find the decimal equivalent: $h = 4.8$

In this case, the easiest way to solve is using the formula for the area of a triangle where $b$ represents the $x$-coordinate of point $Q$, and the variable $h$ represents the $y$-coordinate of $z$:
$\text{Area} = \frac{1}{2}bh$
$12 = \frac{1}{2}5h$
Multiply both sides by 2:
$24 = 5h$
Divide both sides by 5:
$h = \dfrac{24}{5}$
Use long division to find the decimal equivalent: $h = 4.8$
Question 17 |
If $−3$ is one solution of the equation $x^2 + 3x + z = 12$, where $z$ is a constant, what is the other solution?
$0$ | |
$3$ | |
$6$ | |
$9$ |
Question 17 Explanation:
The correct answer is (A). Given that $x = −3$ is a solution, substitute this value for $x$ in the equation to solve for $z$. Substitute the calculated value of $z$ back into the original equation and solve for $x$:
$(−3)^2 + 3(−3) + z = 12$
$9 − 9 + z = 12$
$z = 12$
Substitute this value into the original equation:
$x^2 + 3x + 12 = 12$
$→ x^2 + 3x = 0$
$→ x(x + 3) = 0$
$x = 0 \;$ and $\; x = −3$
$(−3)^2 + 3(−3) + z = 12$
$9 − 9 + z = 12$
$z = 12$
Substitute this value into the original equation:
$x^2 + 3x + 12 = 12$
$→ x^2 + 3x = 0$
$→ x(x + 3) = 0$
$x = 0 \;$ and $\; x = −3$
Question 18 |
An equation of the line that contains the origin and the point $(−4, 7)$ is
$y = \left(-\frac{7}{4}\right)x$ | |
$y = \left(-\frac{4}{7}\right)x$ | |
$y = \left(\frac{7}{4}\right)x$ | |
$y = \left(-\frac{7}{4}\right)x + 2$ |
Question 18 Explanation:
The correct answer is (A). The slope-intercept form of the equation of a line in the coordinate plane is $y = mx + b$, where $b$ is the $y$-intercept and $m$ is the slope.
Since the line passes through the origin $(0, 0)$, the $y$-intercept will be $0$, so the equation will simply read: $y = mx$. Immediately, we can eliminate all answer choices that do not have $0$ as the $y$-intercept.
Recall that:
$m = \text{Slope} = \dfrac{\text{Rise}}{\text{Run}}$
(Or the change in the $y$-coordinates divided by the change in the $x$-coordinates.)
Our two coordinates are $(0, 0)$ and $(-4, 7)$. The slope is:
$m = \dfrac{7 − 0}{−4 − 0} = −\dfrac{7}{4}$
And the equation of the line is:
$y = -\dfrac{7}{4}x$
Since the line passes through the origin $(0, 0)$, the $y$-intercept will be $0$, so the equation will simply read: $y = mx$. Immediately, we can eliminate all answer choices that do not have $0$ as the $y$-intercept.
Recall that:
$m = \text{Slope} = \dfrac{\text{Rise}}{\text{Run}}$
(Or the change in the $y$-coordinates divided by the change in the $x$-coordinates.)
Our two coordinates are $(0, 0)$ and $(-4, 7)$. The slope is:
$m = \dfrac{7 − 0}{−4 − 0} = −\dfrac{7}{4}$
And the equation of the line is:
$y = -\dfrac{7}{4}x$
Question 19 |
If $\;x = p^2\;$ and $\;y = \sqrt{p}\;$ what is the value of $\;x^2y^2 + (xy)^2\;$?
$p^{10}$ | |
$2p^{10}$ | |
$p^5$ | |
$2p^5$ |
Question 19 Explanation:
The correct answer is (D). Recall the rules of combining exponents of the same base:
$x^a \ast x^b = x^{a + b}$
$\sqrt{x} = x^{\frac{1}{2}}$
$(x^a)^b = x^{a \ast b}$
Substitute the values of $x$ and $y$ into the expression and evaluate:
$x^2y^2 + (xy)^2$
$= (p^2)^2 (\sqrt{p})^2 + \left((p^2)(\sqrt{p})\right)^2$
$= (p^2)^2 (\sqrt{p})^2 + (p^2)^2 (\sqrt{p})^2$
$= p^4 \ast p + p^4 \ast p$
$= p^5 + p^5 = 2p^5$
$x^a \ast x^b = x^{a + b}$
$\sqrt{x} = x^{\frac{1}{2}}$
$(x^a)^b = x^{a \ast b}$
Substitute the values of $x$ and $y$ into the expression and evaluate:
$x^2y^2 + (xy)^2$
$= (p^2)^2 (\sqrt{p})^2 + \left((p^2)(\sqrt{p})\right)^2$
$= (p^2)^2 (\sqrt{p})^2 + (p^2)^2 (\sqrt{p})^2$
$= p^4 \ast p + p^4 \ast p$
$= p^5 + p^5 = 2p^5$
Question 20 |
$f(x) = \sqrt{x} − 40$, for all positive values of $x$. If $a = f(b)$ for some positive numbers $b$ and $a$, then what is $b$ in terms of $a$?
$\sqrt{a + 40}$ | |
$(a + 40)^2$ | |
$\sqrt{a^2 + 40}$ | |
$\left(a^2 + 40\right)$ |
Question 20 Explanation:
The correct answer is (B). The question provides the condition that:
$a = f(b)$ and that $f(x) = \sqrt{x} − 40$.
These conditions can be combined to yield:
$a = f(b)$
$a = \sqrt{b} − 40$.
Solving this resulting equation for the variable $b$:
$a = \sqrt{b} − 40$
$a + 40 = \sqrt{b}$
$(a + 40)^2 = (\sqrt{b})^2$
$(a + 40)^2 = b$
$a = f(b)$ and that $f(x) = \sqrt{x} − 40$.
These conditions can be combined to yield:
$a = f(b)$
$a = \sqrt{b} − 40$.
Solving this resulting equation for the variable $b$:
$a = \sqrt{b} − 40$
$a + 40 = \sqrt{b}$
$(a + 40)^2 = (\sqrt{b})^2$
$(a + 40)^2 = b$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
