ACCUPLACER AAF Test Prep
If you are serious about getting a great score on your Accuplacer AAF test, try out our recommended Accuplacer AAF Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The length of a rectangle is four more than its width. If the area of the rectangle is 12, find the length of the rectangle.
$-6$ | |
$2$ | |
$4.5$ | |
$6$ |
Question 1 Explanation:
The correct choice is (D). Since the length of the rectangle is four more than the rectangle’s width, we can write $l$ as $w + 4$.
Substituting in $w + 4$ for $l$ and $12$ for $A$ into the equation $A = l × w$, we get $12 = w(w + 4)$.
Simplifying, we get $12 = w^2 + 4w$.
Subtracting $12$ from both sides, we get $0 = w^2 + 4w - 12$, which can be factored as $(w + 6)(w - 2) = 0$.
Since $w$ must be positive, we equate $w - 2$ to $0$ to get $w = 2$. Since $l = w + 4$, we find that $l = 6$.
Substituting in $w + 4$ for $l$ and $12$ for $A$ into the equation $A = l × w$, we get $12 = w(w + 4)$.
Simplifying, we get $12 = w^2 + 4w$.
Subtracting $12$ from both sides, we get $0 = w^2 + 4w - 12$, which can be factored as $(w + 6)(w - 2) = 0$.
Since $w$ must be positive, we equate $w - 2$ to $0$ to get $w = 2$. Since $l = w + 4$, we find that $l = 6$.
Question 2 |
$\$1.75$ | |
$\$2.00$ | |
$\$3.50$ | |
$\$7.00$ |
Question 2 Explanation:
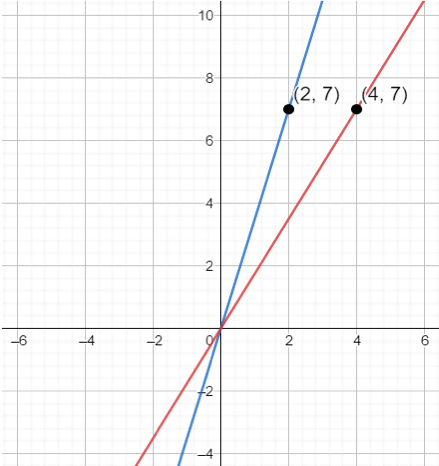
The correct choice is (A). We first find the equation of Chandan’s taxi service. First we find the slope, which is equal to:
$\dfrac{7 - 0 \, \text{ dollars}}{2 - 0 \, \text{ kilometers}}$ $= 3.5 \dfrac{\$}{\text{km}}$ $\text{or } \$3.5 \text{ per km}$
Next, we find the equation of Taylor’s taxi service. We find the slope, which is equal to:
$\dfrac{7 - 0 \, \text{ dollars}}{4 - 0 \, \text{ kilometers}}$ $= 1.75 \dfrac{\$}{\text{km}}$ $\text{or } \$1.75 \text{ per km}$
To find how much more Chandan’s taxi service costs than Taylor’s taxi service, we find $3.5 - 1.75 = \$1.75$ per kilometer.
$\dfrac{7 - 0 \, \text{ dollars}}{2 - 0 \, \text{ kilometers}}$ $= 3.5 \dfrac{\$}{\text{km}}$ $\text{or } \$3.5 \text{ per km}$
Next, we find the equation of Taylor’s taxi service. We find the slope, which is equal to:
$\dfrac{7 - 0 \, \text{ dollars}}{4 - 0 \, \text{ kilometers}}$ $= 1.75 \dfrac{\$}{\text{km}}$ $\text{or } \$1.75 \text{ per km}$
To find how much more Chandan’s taxi service costs than Taylor’s taxi service, we find $3.5 - 1.75 = \$1.75$ per kilometer.
Question 3 |
$f(x) = 5x(x + 3)$. Which of the following is $f(x − 3)$?
$5x^2 − 15x$ | |
$0$ | |
$5x^2$ | |
$5x^2 + 15x$ |
Question 3 Explanation:
The correct choice is (A). To find $f(x − 3)$, we need to substitute $(x − 3)$ for $x$.
$f(x) = 5x(x + 3)$
$f(x − 3) = 5(x − 3)((x − 3) + 3)$
$f(x − 3) = 5(x − 3)(x − 3 + 3)$
$f(x − 3) = 5(x − 3)(x)$
$f(x − 3) = (5x − 15)(x)$
$f(x − 3) = 5x^2 − 15x$
$f(x) = 5x(x + 3)$
$f(x − 3) = 5(x − 3)((x − 3) + 3)$
$f(x − 3) = 5(x − 3)(x − 3 + 3)$
$f(x − 3) = 5(x − 3)(x)$
$f(x − 3) = (5x − 15)(x)$
$f(x − 3) = 5x^2 − 15x$
Question 4 |
Which of the following is equivalent to $(8^x)^{3x} = 24$ where $x ≥ 0$?
$x = \dfrac{\log_8 24}{4}$ | |
$x = \dfrac{3}{4}$ | |
$x = \sqrt{\dfrac{\log_8 24}{3}}$ | |
$x = \sqrt{\dfrac{\log_3 24}{8}}$ |
Question 4 Explanation:
The correct choice is (C). The equation $(8^x)^{3x} = 24$ can be simplified to $8^{3x^2} = 24$.
We can rewrite this as:
$\require{cancel} \cancel{\log_8}(\cancel{8}^{3x^2}) = \log_8 (24)$
$3x^2 = \log_8 24$
Solving for $x$, we get: $x = \sqrt{\dfrac{\log_8 24}{3}}$
We can rewrite this as:
$\require{cancel} \cancel{\log_8}(\cancel{8}^{3x^2}) = \log_8 (24)$
$3x^2 = \log_8 24$
Solving for $x$, we get: $x = \sqrt{\dfrac{\log_8 24}{3}}$
Question 5 |
$2π + 20$ | |
$2π + 16$ | |
$8π + 16$ | |
$8π + 20$ |
Question 5 Explanation:
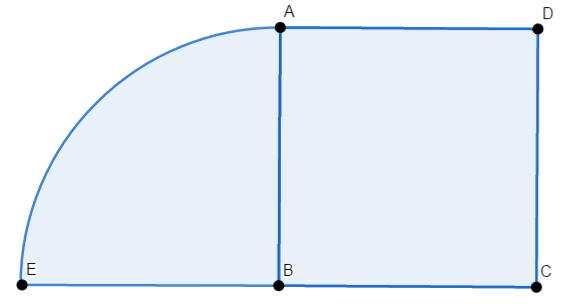
The correct choice is (B). Since square $ABCD$ has an area of $16 \text{m}^2$, it has a side length of $4\text{m}$. Therefore:
$AD + DC + CB + BE$ $= 4 × 4 = 16$
Next, we find the perimeter of the quarter-circle which is equivalent to:
$\dfrac{2π(4)}{4} = 2π$
Summing up, the perimeter of the entire figure is $2π + 16$.
$AD + DC + CB + BE$ $= 4 × 4 = 16$
Next, we find the perimeter of the quarter-circle which is equivalent to:
$\dfrac{2π(4)}{4} = 2π$
Summing up, the perimeter of the entire figure is $2π + 16$.
Question 6 |
Which of the following is the correct factorization of $5x^2 − 15x − 50$?
$(5x + 5)(x − 10)$ | |
$5(x − 5)(x + 2)$ | |
$(5x − 5)(x + 10)$ | |
$5(x − 2)(x + 5)$ |
Question 6 Explanation:
The correct choice is (B). When factoring quadratics, begin by factoring out any common factor of the coefficients:
$5(x^2 − 3x − 10)$
Then factor the "simplified" quadratic:
$5(x − 5)(x + 2)$
$5(x^2 − 3x − 10)$
Then factor the "simplified" quadratic:
$5(x − 5)(x + 2)$
Question 7 |
Which of the following is equivalent to $f(x) = \dfrac{x^2 + 2x − 15}{x^2 − x − 6}$ as long as $x ≠ 3$ and $x ≠ − 2$?
$\dfrac{x − 3}{x + 2}$ | |
$\dfrac{x + 5}{x − 3}$ | |
$\dfrac{x − 3}{x − 6}$ | |
$\dfrac{x + 5}{x + 2}$ |
Question 7 Explanation:
The correct choice is (D). As a general rule, when dealing with rational functions, begin by factoring the numerator and denominator.
$\dfrac{(x + 5)(x − 3)}{(x − 3)(x + 2)}$ $= \require{cancel} \dfrac{(x + 5) \cancel{(x − 3)}}{(\cancel{x − 3})(x + 2)}$ $= \dfrac{x + 5}{x + 2}$
$\dfrac{(x + 5)(x − 3)}{(x − 3)(x + 2)}$ $= \require{cancel} \dfrac{(x + 5) \cancel{(x − 3)}}{(\cancel{x − 3})(x + 2)}$ $= \dfrac{x + 5}{x + 2}$
Question 8 |
What are the solutions to the following equation?
$(2x + \sqrt{2})(5x + \sqrt{19})$ $= 0$$x = \dfrac{-\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{-\sqrt{19}}{5}$ | |
$x = \dfrac{\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{\sqrt{19}}{5}$ | |
$x = \dfrac{-\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{\sqrt{19}}{5}$ | |
$x = \dfrac{\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{-\sqrt{19}}{5}$ |
Question 8 Explanation:
The correct choice is (A). Using the zero product property, we set $(2x + \sqrt{2})$ equal to $0$ and $(5x + \sqrt{19})$ equal to $0$.
Solving $2x + \sqrt{2} = 0$, we get: $x = \dfrac{-\sqrt{2}}{2}$
Solving $5x + \sqrt{19} = 0$, we get: $x = \dfrac{-\sqrt{19}}{5}$
Therefore, the zeroes of the equation are:
$x = \dfrac{-\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{-\sqrt{19}}{5}$
Solving $2x + \sqrt{2} = 0$, we get: $x = \dfrac{-\sqrt{2}}{2}$
Solving $5x + \sqrt{19} = 0$, we get: $x = \dfrac{-\sqrt{19}}{5}$
Therefore, the zeroes of the equation are:
$x = \dfrac{-\sqrt{2}}{2}$ $\text{ and }$ $\dfrac{-\sqrt{19}}{5}$
Question 9 |
$\dfrac{23}{17}$ | |
$\dfrac{7}{15}$ | |
$\dfrac{8}{15}$ | |
$\dfrac{15}{17}$ |
Question 9 Explanation:
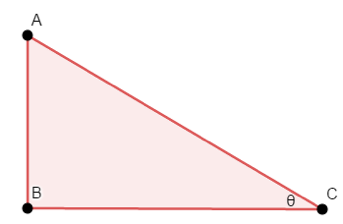
The correct choice is (A). Since the tangent of a triangle can be found by dividing the length of the side opposite to the angle $θ$ by the length of the side adjacent to the angle $θ$. The problem states that $\tan θ = \frac{8}{15}$, which means that $AB = 8$ and $BC = 15$.
The problem also states that the problem is a right triangle, which means that $AC = \sqrt{8^2 + 15^2} = 17$ via the Pythagorean theorem.
Next, we find:
$\sin θ =$ $\dfrac{ \text{Length of side opposite to } θ}{\text{Length of hypotenuse}}$ $= \dfrac{8}{17}$
$\cos θ =$ $\dfrac{\text{Length of side adjacent to } θ}{\text{Length of hypotenuse}}$ $= \dfrac{15}{17}$
Adding $\sin θ$ to $\cos θ$, we get: $\dfrac{8}{17} + \dfrac{15}{17} = \dfrac{23}{17}$
The problem also states that the problem is a right triangle, which means that $AC = \sqrt{8^2 + 15^2} = 17$ via the Pythagorean theorem.
Next, we find:
$\sin θ =$ $\dfrac{ \text{Length of side opposite to } θ}{\text{Length of hypotenuse}}$ $= \dfrac{8}{17}$
$\cos θ =$ $\dfrac{\text{Length of side adjacent to } θ}{\text{Length of hypotenuse}}$ $= \dfrac{15}{17}$
Adding $\sin θ$ to $\cos θ$, we get: $\dfrac{8}{17} + \dfrac{15}{17} = \dfrac{23}{17}$
Question 10 |
$AB ≅ ED$ | |
$∠ACB ≅ ∠ECD$ | |
$CD ≅ CE$ | |
$BC ≅ DC$ |
Question 10 Explanation:
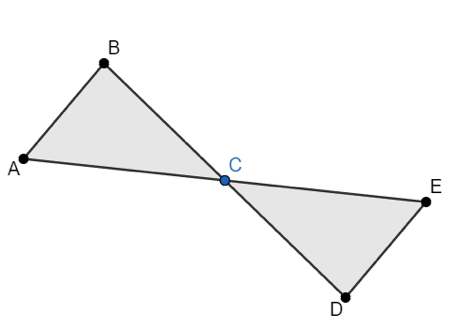
The correct choice is (D). First, we know that $∠BCA ≅ ∠DCE$ since they are vertical angles. We are also given that $AC ≅ EC$.
Looking at choice (D), we see that if $BC ≅ DC$, triangles $ABC$ and $EDC$ would be congruent using the Side-Angle-Side postulate.
Looking at choice (D), we see that if $BC ≅ DC$, triangles $ABC$ and $EDC$ would be congruent using the Side-Angle-Side postulate.
Question 11 |
If $x > 0$ and $y > 0$, which of the following expressions is equivalent to $\dfrac{\sqrt{x} + \sqrt{y}}{xy}$?
$\dfrac{\sqrt{x + y}}{xy}$ | |
$\dfrac{x + y}{\sqrt{x + y}}$ | |
$\dfrac{1}{y\sqrt{x}} + \dfrac{1}{x\sqrt{y}}$ | |
$\dfrac{1}{\sqrt{xy}}$ |
Question 11 Explanation:
The correct choice is (C).
The expression $\dfrac{\sqrt{x} + \sqrt{y}}{xy}$ can be separated into: $\dfrac{\sqrt{x}}{xy} + \dfrac{\sqrt{y}}{xy}$
This expression can be rewritten as:
$\dfrac{x^{\frac{1}{2}}}{xy} + \dfrac{y^{\frac{1}{2}}}{xy}$ $= \dfrac{1}{(x^{1 − \frac{1}{2}})(y)}$ $+ \dfrac{1}{(x)(y^{1 − \frac{1}{2}})}$
$= \dfrac{1}{(x^{\frac{1}{2}})(y)}$ $+ \dfrac{1}{(x)(y^{\frac{1}{2}})}$ $= \dfrac{1}{y\sqrt{x}} + \dfrac{1}{x\sqrt{y}}$
An alternate approach:
$\dfrac{\sqrt{x}}{xy} + \dfrac{\sqrt{y}}{xy}$ $= \dfrac{\cancel{\sqrt{x}}}{\cancel{\sqrt{x}} \sqrt{x} y} + \dfrac{\cancel{\sqrt{y}}}{x \cancel{\sqrt{y}}\sqrt{y}}$
$= \dfrac{1}{\sqrt{x} y} + \dfrac{1}{x\sqrt{y}}$
The expression $\dfrac{\sqrt{x} + \sqrt{y}}{xy}$ can be separated into: $\dfrac{\sqrt{x}}{xy} + \dfrac{\sqrt{y}}{xy}$
This expression can be rewritten as:
$\dfrac{x^{\frac{1}{2}}}{xy} + \dfrac{y^{\frac{1}{2}}}{xy}$ $= \dfrac{1}{(x^{1 − \frac{1}{2}})(y)}$ $+ \dfrac{1}{(x)(y^{1 − \frac{1}{2}})}$
$= \dfrac{1}{(x^{\frac{1}{2}})(y)}$ $+ \dfrac{1}{(x)(y^{\frac{1}{2}})}$ $= \dfrac{1}{y\sqrt{x}} + \dfrac{1}{x\sqrt{y}}$
An alternate approach:
$\dfrac{\sqrt{x}}{xy} + \dfrac{\sqrt{y}}{xy}$ $= \dfrac{\cancel{\sqrt{x}}}{\cancel{\sqrt{x}} \sqrt{x} y} + \dfrac{\cancel{\sqrt{y}}}{x \cancel{\sqrt{y}}\sqrt{y}}$
$= \dfrac{1}{\sqrt{x} y} + \dfrac{1}{x\sqrt{y}}$
Question 12 |
Which of the following equations has a slope parallel to $y = \dfrac{1}{2}(x + 3)$ and passes through the point $(3, 16)$?
$y = -2x + \dfrac{29}{2}$ | |
$y = 2x + \dfrac{3}{2}$ | |
$y = \dfrac{1}{2}x + \dfrac{29}{2}$ | |
$y = -\dfrac{1}{2}x + \dfrac{3}{2}$ |
Question 12 Explanation:
The correct choice is (C). A line parallel to one with the equation of $y = \frac{1}{2}(x + 3)$ has a slope of $\frac{1}{2}$.
Applying the point-slope formula to find the equation of the line that passes through $(3, 16)$, we get $y - 16 = \frac{1}{2}(x - 3)$, which can be simplified to $y = \frac{1}{2}x + \frac{29}{2}$.
Applying the point-slope formula to find the equation of the line that passes through $(3, 16)$, we get $y - 16 = \frac{1}{2}(x - 3)$, which can be simplified to $y = \frac{1}{2}x + \frac{29}{2}$.
Question 13 |
Which of the following are the solutions to $3x^2 + 9x + 12 = 0$?
Express $\sqrt{-1}$ as i.$- \dfrac{3}{2} ± \dfrac{i\sqrt{7}}{2}$ | |
$\dfrac{3}{2} ± \dfrac{3i\sqrt{7}}{2}$ | |
$- \dfrac{3}{2} ± \dfrac{\sqrt{51}}{6}$ | |
$\dfrac{3}{2} ± \dfrac{-i\sqrt{23}}{2}$ |
Question 13 Explanation:
The correct choice is (A). We can apply the quadratic formula to $3x^2 + 9x + 12 = 0$.
Plugging in 3, 9, and 12 for $a$,$b$, and $c$ respectively into:
$\dfrac{-b ± \sqrt{b^2 - 4ac}}{2a}$, we get:
$\dfrac{-9 ± \sqrt{-63}}{6}$ $= \dfrac{-9 ± \sqrt{-1 × 9 × 7}}{6}$
$= \dfrac{-9 ± \sqrt{9 × -1 × 7}}{6}$ $= \dfrac{-9 ± \sqrt{9} \sqrt{-1} \sqrt{7}}{6}$
$= \dfrac{-9 ± 3i \sqrt{7}}{6}$ $= -\dfrac{9}{6} ± \dfrac{3i\sqrt{7}}{6}$
$= -\dfrac{3}{2} ± \dfrac{i\sqrt{7}}{2}$
Plugging in 3, 9, and 12 for $a$,$b$, and $c$ respectively into:
$\dfrac{-b ± \sqrt{b^2 - 4ac}}{2a}$, we get:
$\dfrac{-9 ± \sqrt{-63}}{6}$ $= \dfrac{-9 ± \sqrt{-1 × 9 × 7}}{6}$
$= \dfrac{-9 ± \sqrt{9 × -1 × 7}}{6}$ $= \dfrac{-9 ± \sqrt{9} \sqrt{-1} \sqrt{7}}{6}$
$= \dfrac{-9 ± 3i \sqrt{7}}{6}$ $= -\dfrac{9}{6} ± \dfrac{3i\sqrt{7}}{6}$
$= -\dfrac{3}{2} ± \dfrac{i\sqrt{7}}{2}$
Question 14 |
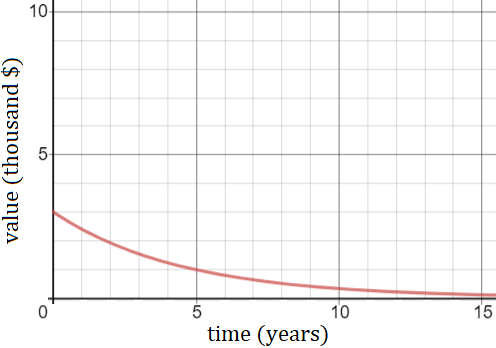
$\text{The}$ $\text{initial}$ $\text{value}$ $\text{of}$ $\text{the}$ $\text{bike}$ $\text{is}$ $\$300$ | |
$\text{The}$ $\text{value}$ $\text{of}$ $\text{the}$ $\text{bike}$ $\text{approaches}$ $\$0$ $\text{as}$ $\text{time}$ $\text{progresses.}$ | |
$\text{The}$ $\text{value}$ $\text{of}$ $\text{the}$ $\text{bike}$ $\text{is}$ $\text{stagnant}$ $\text{after}$ $\text{year}$ $5.$ | |
$\text{The}$ $\text{total}$ $\text{value}$ $\text{of}$ $\text{the}$ $\text{bike}$ $\text{is}$ $15$ $\text{thousand}$ $\text{dollars.}$ |
Question 14 Explanation:
The correct choice is (B). Based on the graph, we see that initially (t = 0) the bike has a value of \$3,000. After 5 years (t = 5), the bike's value is approximately \$1,000. As time progresses, the bike’s value approaches \$0.
Question 15 |
Which of the following is true of the function shown below?
$f(x) =$ $-0.7x^3 + 3.14x^2$ $ +\, 6.28x + 121$$\text{It}$ $\text{has}$ $\text{a}$ $\text{degree}$ $\text{of}$ $6,$ $\text{and}$ $\text{as}$ $x$ $\text{approaches}$ $∞,$ $y$ $\text{approaches}$ $-∞.$ | |
$\text{It}$ $\text{has}$ $\text{an}$ $\text{even}$ $\text{degree},$ $\text{and}$ $\text{as}$ $y$ $\text{approaches}$ $∞,$ $x$ $\text{approaches}$ $-∞.$ | |
$\text{It}$ $\text{has}$ $\text{a}$ $\text{degree}$ $\text{of}$ $3,$ $\text{and}$ $\text{as}$ $x$ $\text{approaches}$ $∞,$ $y$ $\text{approaches}$ $-∞.$ | |
$\text{It}$ $\text{has}$ $\text{a}$ $\text{prime}$ $\text{degree},$ $\text{and}$ $\text{as}$ $x$ $\text{approaches}$ $∞,$ $y$ $\text{approaches}$ $∞.$ |
Question 15 Explanation:
The correct choice is (C). Examining the function above, we know that its degree is odd and it has a negative leading coefficient.
In functions that have odd degrees and negative leading coefficients, as $x$ approaches ∞, $y$ approaches -∞, and as $x$ approaches -∞, $y$ approaches ∞. Thus, the only choice that correctly identifies the degree and the end behavior of the graph is choice C.
In functions that have odd degrees and negative leading coefficients, as $x$ approaches ∞, $y$ approaches -∞, and as $x$ approaches -∞, $y$ approaches ∞. Thus, the only choice that correctly identifies the degree and the end behavior of the graph is choice C.
Question 16 |
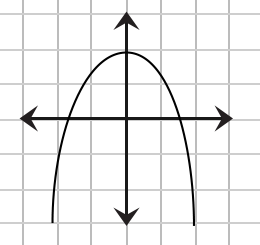
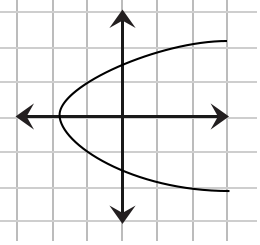
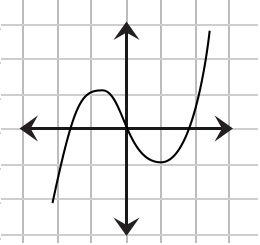
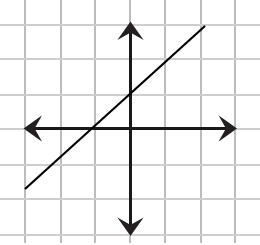
Which of the following depicts a one-to-one function?
 | |
 | |
 | |
 |
Question 16 Explanation:
The correct choice is (D). To be a function, the graph of the relation must pass the vertical line test. Graph (B) fails the vertical line test, but (A), (C), and (D) pass.
To be a one-to-one function, the graph of the function must pass the horizontal line test. Only graph (D) passes.
To be a one-to-one function, the graph of the function must pass the horizontal line test. Only graph (D) passes.
Question 17 |
$8$ | |
$4$ | |
$2$ | |
$-2$ |
Question 17 Explanation:
The correct choice is (C). First, we find the value of $z(-8)$ which is $4$. Next, we plug $4$ back into the function. We are left to find $z(4)$ which is equal to $2$.
Question 18 |
For an acute angle, $x$, which of the following is guaranteed to be greater than $1$?
$\sin(x)$ | |
$\cos(x)$ | |
$\tan(x)$ | |
$\dfrac{1}{\cos(x)}$ |
Question 18 Explanation:
The correct choice is (D). $\sin(x)$ and $\cos(x)$ can never be greater than $1$, regardless of the angle.
$\tan(x)$ will exceed $1$ for acute angles exceeding $45°$, but will be less than $1$ for acute angles less than $45°$.
$\cos(x)$ will be less than $1$ for all acute angles. This means that $\dfrac{1}{\cos(x)}$ is guaranteed to be greater than $1$ for the same angles.
For example, the $\cos(30°) = \dfrac{1}{2}$, therefore $\dfrac{1}{\cos(30°)} = \dfrac{1}{\frac{1}{2}}$ $= 1 \cdot \dfrac{2}{1} = 2$.
$\tan(x)$ will exceed $1$ for acute angles exceeding $45°$, but will be less than $1$ for acute angles less than $45°$.
$\cos(x)$ will be less than $1$ for all acute angles. This means that $\dfrac{1}{\cos(x)}$ is guaranteed to be greater than $1$ for the same angles.
For example, the $\cos(30°) = \dfrac{1}{2}$, therefore $\dfrac{1}{\cos(30°)} = \dfrac{1}{\frac{1}{2}}$ $= 1 \cdot \dfrac{2}{1} = 2$.
Question 19 |
Which of the following provides the domain of $y = \dfrac{37}{\sqrt{x + 2}}$?
$x > 0$ | |
$x > −2$ | |
$x < −2$ | |
$x < 2$ |
Question 19 Explanation:
The correct choice is (B). The domain represents all values of $x$, the input, for which a value of $y$, the output, exists.
We cannot have a negative under a square root and we cannot divide by $0$.
This means $x + 2 > 0$ and, when cancelling out the $2$ by subtracting it from both sides, $x > −2$.
We cannot have a negative under a square root and we cannot divide by $0$.
This means $x + 2 > 0$ and, when cancelling out the $2$ by subtracting it from both sides, $x > −2$.
Question 20 |
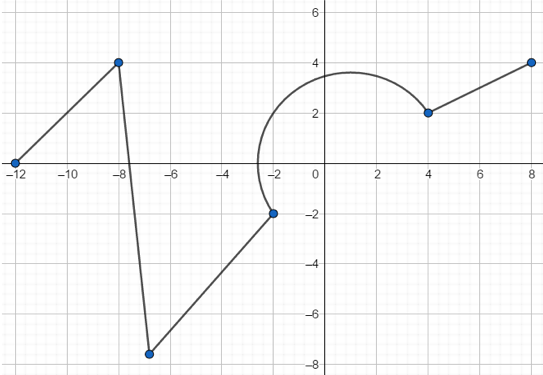
A quadratic function has roots at $(-3, 0)$ and $(5, 0)$. Which of the following could represent the minimum point of the function?
$(1, -16)$ | |
$(1.5, -16)$ | |
$(2, -16)$ | |
$(1, 0)$ |
Question 20 Explanation:
The correct choice is (A). We are given that the two zeroes of the graph are $(-3, 0)$ and $(5, 0)$, which means that the minimum point of the function has an $x$ value of $\dfrac{-3 + 5}{2} = 1$.
The equation of this parabola is $y = (x + 3)(x - 5)$ from the given roots. This means the $y$-value of the parabola at $x = 1$ is $(1 + 3)(1 - 5) = -16$. Therefore, the correct answer is $(1, -16)$.
The equation of this parabola is $y = (x + 3)(x - 5)$ from the given roots. This means the $y$-value of the parabola at $x = 1$ is $(1 + 3)(1 - 5) = -16$. Therefore, the correct answer is $(1, -16)$.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |