ACCUPLACER QAS Test Prep
If you are serious about getting a great score on your Accuplacer QAS test, try out our recommended Accuplacer QAS Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $y + 3y + 5y = −18$, then what is the value of $y$?
$1$ | |
$−2$ | |
$0$ | |
$−1$ |
Question 1 Explanation:
The correct choice is (B). When terms with the same variable are in the same equation, they can be combined:
$y + 3y + 5y = −18$
$9y = −18$
$y = \dfrac{−18}{9}$
$y = −2$
$y + 3y + 5y = −18$
$9y = −18$
$y = \dfrac{−18}{9}$
$y = −2$
Question 2 |
Which of the following expressions is equivalent to $(x^7y^3)^5$?
$x^{12}y^8$ | |
$x^{35}y^8$ | |
$x^8y^{12}$ | |
$x^{35}y^{15}$ |
Question 2 Explanation:
The correct choice is (D). The power is distributed to each term in the parenthesis:
$(x^7 × y^3 )^5 = x^{7 × 5}y^{3 × 5} = x^{35} y^{15}$
$(x^7 × y^3 )^5 = x^{7 × 5}y^{3 × 5} = x^{35} y^{15}$
Question 3 |
Let $X$ and $Y$ be the following sets:
$X = \{2, 8, 10, 11, 13, 16, 17\}$$Y = \{1, 5, 7, 11, 13\}$ Which of the following is the set $X ∩ Y$?
$\{11, 13\}$ | |
$\{13\}$ | |
$\{1, 5, 7, 11, 13\}$ | |
$\{1, 2, 5, 7, 8, 10, 11, 13, 16, 17\}$ |
Question 3 Explanation:
The correct choice is (A). The ∪ symbol means union. The union of two sets includes all the values that are in either (or both) of the sets.
The ∩ symbol means intersection. The intersection of a set includes only the numbers that are in both sets. Only two numbers are present in both sets $X$ and $Y$:
$\{11, 13\}$
The ∩ symbol means intersection. The intersection of a set includes only the numbers that are in both sets. Only two numbers are present in both sets $X$ and $Y$:
$\{11, 13\}$
Question 4 |
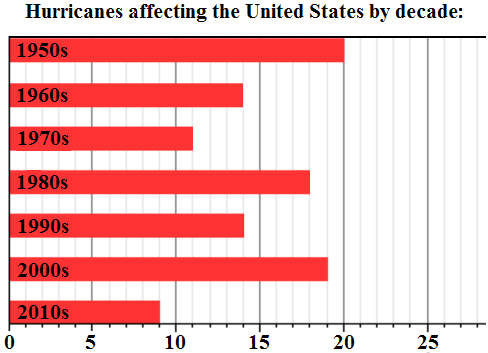
What is the mean number of hurricanes affecting the US per decade?
$13$ | |
$14$ | |
$15$ | |
$18$ |
Question 4 Explanation:
The correct choice is (C). Mean is just another word for average. To find the average, add up all the numbers, then divide by how many numbers there are:
$\text{Average} =$ $\frac{20 + 14 + 11 + 18 + 14 + 19 + 9}{7}$
$\text{Average} = \frac{105}{7} = 15$
$\text{Average} =$ $\frac{20 + 14 + 11 + 18 + 14 + 19 + 9}{7}$
$\text{Average} = \frac{105}{7} = 15$
Question 5 |
What is the solution to the equation $\frac{3}{7}(x + 3) + 5 = 3x + 2$?
$\dfrac{2}{3}$ | |
$\dfrac{5}{3}$ | |
$\dfrac{3}{4}$ | |
$\dfrac{1}{2}$ |
Question 5 Explanation:
The correct choice is (B). Applying the distributive property to the left side, we get:
$\frac{3}{7}x + \frac{9}{7} + 5 = 3x + 2$
Next, bring all the constants to the left side, and all the variables to the right side. Then simplify each side:
$\frac{9}{7} + 5 - 2 = 3x - \frac{3}{7} x$
$\frac{9}{7} + 3 = 3x - \frac{3}{7} x$
$\frac{9}{7} + \frac{21}{7} = \frac{21x}{7} - \frac{3x}{7}$
$\frac{30}{7} = \frac{18x}{7}$
To solve $\frac{18x}{7} = \frac{30}{7}$, we can equate the numerators since the denominators are equivalent, giving us $18x = 30$. Isolating and simplifying, we get:
$x = \frac{30}{18} = \frac{5}{3}$
$\frac{3}{7}x + \frac{9}{7} + 5 = 3x + 2$
Next, bring all the constants to the left side, and all the variables to the right side. Then simplify each side:
$\frac{9}{7} + 5 - 2 = 3x - \frac{3}{7} x$
$\frac{9}{7} + 3 = 3x - \frac{3}{7} x$
$\frac{9}{7} + \frac{21}{7} = \frac{21x}{7} - \frac{3x}{7}$
$\frac{30}{7} = \frac{18x}{7}$
To solve $\frac{18x}{7} = \frac{30}{7}$, we can equate the numerators since the denominators are equivalent, giving us $18x = 30$. Isolating and simplifying, we get:
$x = \frac{30}{18} = \frac{5}{3}$
Question 6 |
Pierre randomly picks out and keeps a marble from a bag that contains 4 red marbles, 7 blue marbles, 9 yellow marbles, and 6 green marbles. Then Antoine picks a marble at random from the same bag. If Pierre’s marble is green, what is the probability that Antoine’s marble will also be green?
$\dfrac{6}{26}$ | |
$\dfrac{5}{26}$ | |
$\dfrac{3}{13}$ | |
$\dfrac{1}{5}$ |
Question 6 Explanation:
The correct choice is (D). Since Pierre keeps his marble, the number of green marbles and the total number of marbles both decrease by 1. So there will be 5 green marbles and 25 total marbles:
Probability = $\dfrac{5}{25} = \dfrac{1}{5}$
Probability = $\dfrac{5}{25} = \dfrac{1}{5}$
Question 7 |
A basketball fundraiser was held at the local community center. The chart below shows the results of the free-throw competition. Out of all of the age groups, approximately what percentage of the shots did the 21–30 age group successfully make?
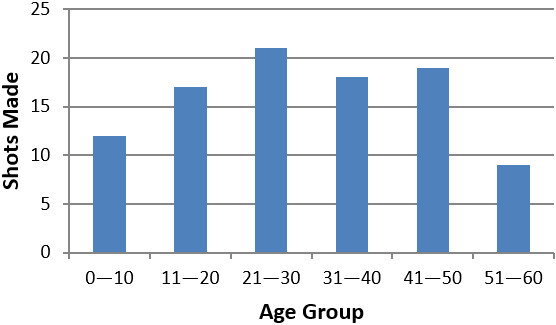
$19\%$ | |
$18\%$ | |
$25\%$ | |
$22\%$ |
Question 7 Explanation:
The correct choice is (D). We first calculate the total number of shot made by all of the age groups. Using estimation, we can say that the total shots made equal:
$12 + 17 + 21 + 18 + 19 + 9$ $= 96$
The 21–30 age group made 21 shots. Therefore:
$\frac{21}{96} × 100 ≈ 22\%$
$12 + 17 + 21 + 18 + 19 + 9$ $= 96$
The 21–30 age group made 21 shots. Therefore:
$\frac{21}{96} × 100 ≈ 22\%$
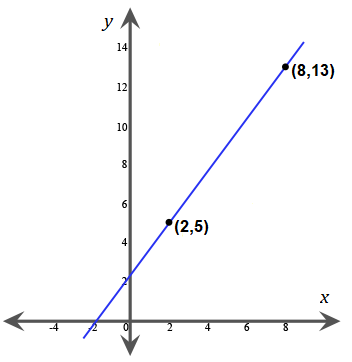
Question 8 |
$y = \dfrac{4}{3}x + 7$ | |
$y = 2x + 7$ | |
$y = 5x + 8$ | |
$y = \dfrac{3}{4}x + \dfrac{7}{3}$ |
Question 8 Explanation:
The correct choice is (A). Use the slope formula:
$\text{Slope} = \dfrac{\text{Change in } y}{\text{Change in } x}$ $= \dfrac{y_2 - y_1}{x_2 - x_1}$
The slope of the line that is pictured is:
$\dfrac{13-5}{8-2} = \dfrac{8}{6} = \dfrac{4}{3}$
Each of the answer choices is written in slope-intercept form, $y = mx + b$, where $m$ is the slope. Choice (A) has a slope of $\frac{4}{3}$, so (A) is correct.
$\text{Slope} = \dfrac{\text{Change in } y}{\text{Change in } x}$ $= \dfrac{y_2 - y_1}{x_2 - x_1}$
The slope of the line that is pictured is:
$\dfrac{13-5}{8-2} = \dfrac{8}{6} = \dfrac{4}{3}$
Each of the answer choices is written in slope-intercept form, $y = mx + b$, where $m$ is the slope. Choice (A) has a slope of $\frac{4}{3}$, so (A) is correct.
Question 9 |
The weight, in pounds, of a truck with its load is given by the equation below where $w$ represents the total weight of the truck and its load, and $q$ represents the quantity of castings it is hauling. In the equation, what does the number 35,000 represent?
$w = 500q + 35,000$The combined weight of the truck and a full load of castings | |
The weight of the truck with no load | |
The weight of each casting | |
The maximum weight of castings that the truck can haul |
Question 9 Explanation:
The correct choice is (B). We are told that $w$ represents the total weight of the truck and its load, and $q$ represents the quantity of castings it is hauling.
If a truck is hauling no castings, $q = 0$.
When $q = 0$, $w = 500(0) + 35,000 = 35,000$.
In other words, the weight of the truck by itself (i.e. hauling no castings) is 35,000 lbs.
If a truck is hauling no castings, $q = 0$.
When $q = 0$, $w = 500(0) + 35,000 = 35,000$.
In other words, the weight of the truck by itself (i.e. hauling no castings) is 35,000 lbs.
Question 10 |
If Tonya needed to buy 9 bottles of soda for a party in which 12 people attended, how many bottles of soda will she need to buy for a party in which 8 people are attending?
6 | |
8 | |
10 | |
12 |
Question 10 Explanation:
The correct answer is (A). We can set up a proportion to solve:
$\dfrac{9 \text{ bottles}}{12 \text{ people}} = \dfrac {x \text{ bottles}}{8 \text{ people}}$
Cross-multiply to solve a proportion:
$(9)(8) = (12)(x)$
$72 = 12x$
$6 = x$
$\dfrac{9 \text{ bottles}}{12 \text{ people}} = \dfrac {x \text{ bottles}}{8 \text{ people}}$
Cross-multiply to solve a proportion:
$(9)(8) = (12)(x)$
$72 = 12x$
$6 = x$
Question 11 |
Which of the following expressions is equivalent to $3x(2 + 5y)$?
$3x + 5y$ | |
$6x + 5y$ | |
$6x + 15y$ | |
$6x + 15xy$ |
Question 11 Explanation:
The correct choice is (D). Begin by noticing the form in which the answer choices are written. As no answer choice contains a parenthetical expression, start by distributing the $3x$ through the parentheses. Multiply $3x$ by each of the terms inside of the parentheses and combine any like terms:
$3x(2 + 5y)$
$= 3x(2) + 3x(5y)$
$= 6x + 15xy$
$3x(2 + 5y)$
$= 3x(2) + 3x(5y)$
$= 6x + 15xy$
Question 12 |
Line $f$ goes through points $(0, 7)$ and $(3, 5)$ in the $xy$-plane. Line $g$ is perpendicular to line $f$. Which of the following is the slope of line $g$?
$-\dfrac{2}{3}$ | |
$-\dfrac{3}{2}$ | |
$\dfrac{3}{2}$ | |
$\dfrac{2}{3}$ |
Question 12 Explanation:
The correct choice is (C). First use the slope forumula to find the slope of line $f$:
$\dfrac{5 - 7}{3 - 0} = - \dfrac{2}{3}$
A line perpendicular to another has a slope that is the negative reciprocal of the slope of the other line. The negative reciprocal of $-\dfrac{2}{3}$ is $\dfrac{3}{2}$.
$\dfrac{5 - 7}{3 - 0} = - \dfrac{2}{3}$
A line perpendicular to another has a slope that is the negative reciprocal of the slope of the other line. The negative reciprocal of $-\dfrac{2}{3}$ is $\dfrac{3}{2}$.
Question 13 |
Solve for x:
$3(x + 1) = 5(x − 2) + 7$$3$ | |
$−3$ | |
$2$ | |
$−2$ |
Question 13 Explanation:
The correct choice is (A). Begin by distributing the 3 and the 5 through their respective parentheses, then combine like terms on each side of the equal sign:
$3(x + 1) = 5(x − 2) + 7$
$3x + 3 = 5x − 10 + 7$
$3x + 3 = 5x − 3$
Add 3 to both sides to maintain the equality:
$3x + 6 = 5x$
Subtract 3$x$ from both sides and then divide the resulting equation by 2 to solve for $x$ as follows:
$6 = 2x$
$3 = x$
Remember that any time a variable is solved for in an equation, the calculated value can be verified by substituting it into the original equation and determining whether it yields a true statement.
$3(x + 1) = 5(x − 2) + 7$
$3x + 3 = 5x − 10 + 7$
$3x + 3 = 5x − 3$
Add 3 to both sides to maintain the equality:
$3x + 6 = 5x$
Subtract 3$x$ from both sides and then divide the resulting equation by 2 to solve for $x$ as follows:
$6 = 2x$
$3 = x$
Remember that any time a variable is solved for in an equation, the calculated value can be verified by substituting it into the original equation and determining whether it yields a true statement.
Question 14 |
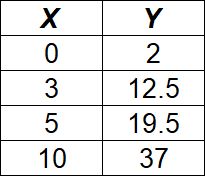
Which of the following best describes the relationship between $X$ and $Y$?
$y = 3.5x + 2$ | |
$y = 10.5x + 2$ | |
$y = 2x + 10.5$ | |
$y = 19.5x + 12.5$ |
Question 14 Explanation:
The correct choice is (A). First use any two points to find the slope. We will use (0, 2) and (3, 12.5):
$\dfrac{12.5 - 2}{3 - 0} = \dfrac{10.5}{3} = 3.5$
The point (0, 2) indicates that the $y$-intercept of the line is 2. Plugging in the slope and $y$-intercept into the $y = mx + b$ form, we get $y = 3.5x + 2$.
$\dfrac{12.5 - 2}{3 - 0} = \dfrac{10.5}{3} = 3.5$
The point (0, 2) indicates that the $y$-intercept of the line is 2. Plugging in the slope and $y$-intercept into the $y = mx + b$ form, we get $y = 3.5x + 2$.
Question 15 |
You are in charge of buying T-shirts for your school’s math club. There are 27 club members, who will each receive a shirt. The T-shirts come in boxes. Each box contains 4 T-shirts and costs \$23.50. What is the total cost for the T-shirts?
$\$164.50$ | |
$\$634.50$ | |
$\$141.00$ | |
$\$150.65$ |
Question 15 Explanation:
The correct choice is (A). There are 27 club members, and each will receive a T-shirt. Each box contains 4 shirts, so:
$\dfrac{27}{4} = 6.75 → 7$
7 boxes of T-shirts will be ordered (since a whole number of boxes must be ordered). Each box costs \$23.50, so the total cost for all the shirts is:
$7 × \$23.50 = \$164.50$
$\dfrac{27}{4} = 6.75 → 7$
7 boxes of T-shirts will be ordered (since a whole number of boxes must be ordered). Each box costs \$23.50, so the total cost for all the shirts is:
$7 × \$23.50 = \$164.50$
Question 16 |
Timothy’s Thrilling Taxi Service charges \$2.50 for the first mile and \$0.75 for each additional mile. How far could a passenger with $10.00 travel?
$11 \text{ miles}$ | |
$10 \text{ miles}$ | |
$9 \text{ miles}$ | |
$7.5 \text{ miles}$ |
Question 16 Explanation:
The correct choice is (A). The initial charge for Timothy’s Taxi Service is \$2.50 for the first mile, with an additional charge of \$0.75 for each additional mile. We can set up an equation with $c$ being the total charge and $m$ being the total number of additional miles traveled:
$c = 2.5 + 0.75m$
Substitute $10$ in for $c$ and solve for $m$:
$10 = 2.5 + 0.75m$
$7.5 = 0.75m$
$m = \frac{7.5}{0.75} = 10$
Add 1 for the first mile traveled. Our answer is 10 + 1 = 11 miles.
$c = 2.5 + 0.75m$
Substitute $10$ in for $c$ and solve for $m$:
$10 = 2.5 + 0.75m$
$7.5 = 0.75m$
$m = \frac{7.5}{0.75} = 10$
Add 1 for the first mile traveled. Our answer is 10 + 1 = 11 miles.
Question 17 |
If $\dfrac{6}{z+4} = p$, and $p = 12$, what is the value of $z $?
$−1.5$ | |
$−3.5$ | |
$1.5$ | |
$3.5$ |
Question 17 Explanation:
The correct choice is (B). Start by substituting 12 for p in the original equation:
$\frac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by 12:
$\frac{6}{12} = z + 4$
Simplify the fraction and then subtract 4:
$\frac{1}{2} = z + 4$
$\frac{1}{2} - 4 = z$
$-3.5 = z$
$\frac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by 12:
$\frac{6}{12} = z + 4$
Simplify the fraction and then subtract 4:
$\frac{1}{2} = z + 4$
$\frac{1}{2} - 4 = z$
$-3.5 = z$
Question 18 |
31 + 20 − 13 = ?
$0$ | |
$2$ | |
$3$ | |
$4$ |
Question 18 Explanation:
The correct choice is (C). Any number raised to the power of 1 equals itself, so 31 is equal to 3.
Any number, except zero, that is raised to the 0 power equals 1, so 20 equals 1.
When 1 is raised to any power it always equals 1. The expression becomes:
$3 + 1 − 1 = 3$
Any number, except zero, that is raised to the 0 power equals 1, so 20 equals 1.
When 1 is raised to any power it always equals 1. The expression becomes:
$3 + 1 − 1 = 3$
Question 19 |
How many imperial gallons are there in 1,400 liters?
Note: 1 kiloliter = 220 imperial gallonsNote: 1,000 liters = 1 kiloliter
$308$ | |
$3{,}080$ | |
$30{,}800$ | |
$308{,}000$ |
Question 19 Explanation:
The correct choice is (A). Solve with dimensional analysis:
$\require{cancel} 1400 \cancel{\text{ liters}} \cdot$ $\dfrac{1 \cancel{\text{ kiloliter}}}{1000 \cancel{\text{liters}}} \cdot$ $\dfrac{ 220 \text{ gallons}}{1 \cancel{\text{kiloliter}}}$
$= \dfrac{(1400)(220)}{1000} \text{ gallons}$ $= 308 \text{ gallons}$
$\require{cancel} 1400 \cancel{\text{ liters}} \cdot$ $\dfrac{1 \cancel{\text{ kiloliter}}}{1000 \cancel{\text{liters}}} \cdot$ $\dfrac{ 220 \text{ gallons}}{1 \cancel{\text{kiloliter}}}$
$= \dfrac{(1400)(220)}{1000} \text{ gallons}$ $= 308 \text{ gallons}$
Question 20 |
List A consists of the numbers {2, 9, 5, 1, 13}, and list B consists of the numbers {7, 4, 12, 15, 18}. If the two lists are combined, what is the median of the combined list?
$6$ | |
$7$ | |
$8$ | |
$9$ |
Question 20 Explanation:
The correct choice is (C). Recall that the median of a set of data is the value located in the middle of the data set. In the case of a data set that contains an even number of numbers, the median is the average of the two middle numbers. Combine the 2 sets provided, and organize them in ascending order:
$\{1, 2, 4, 5, 7, 9, 12, 13, 15, 18\}$
Since there are an even number of items in the resulting list, the median is the average of the two middle numbers.
$\text{Median} =$ $(7 + 9) ÷ 2 = 8$
$\{1, 2, 4, 5, 7, 9, 12, 13, 15, 18\}$
Since there are an even number of items in the resulting list, the median is the average of the two middle numbers.
$\text{Median} =$ $(7 + 9) ÷ 2 = 8$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |