ACCUPLACER Arithmetic Test Prep
If you are serious about getting a great score on your Accuplacer Arithmetic test, try out our recommended Accuplacer Arithmetic Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Which of these decimals is the greatest?
$0.028$ | |
$0.0082$ | |
$0.82$ | |
$0.28$ |
Question 1 Explanation:
The correct choice is (C). To determine which of these four numbers is greatest, look for the largest digit in the tenths place (the first place to the right of the decimal). The correct answer of 0.82 has an “8” in that position, whereas the other answer choices have either a “0” or a “2”.
Question 2 |
On Halloween Mr. Burke brought in 89 mini candy bars and 66 lollipops for his class of 31 students. How many total treats did he bring?
$145$ | |
$186$ | |
$5$ | |
$155$ |
Question 2 Explanation:
The correct choice is (D). Read the word problems carefully. To find the total number of treats simply add the number of mini candy bars and the number of lollipops:
$89 + 66 = 155$
$89 + 66 = 155$
Question 3 |
$\dfrac{7}{8} ÷ \dfrac{9}{5} = ~?$
$\dfrac{7}{40}$ | |
$\dfrac{35}{72}$ | |
$\dfrac{40}{72}$ | |
$\dfrac{63}{40}$ |
Question 3 Explanation:
The correct choice is (B). When dividing fractions, we flip the denominator and change the division sign to a multiplication sign as follows:
$\dfrac{7}{8} ÷ \dfrac{9}{5}$
$= \dfrac{7}{8} \ast \dfrac{5}{9} = \dfrac{7 \ast 5}{8 \ast 9}$ $ = \dfrac{35}{72}$
$\dfrac{7}{8} ÷ \dfrac{9}{5}$
$= \dfrac{7}{8} \ast \dfrac{5}{9} = \dfrac{7 \ast 5}{8 \ast 9}$ $ = \dfrac{35}{72}$
Question 4 |
Add:
$1.728 + 0.9975 + 2.42 =$
$4.1355$ | |
$5.1455$ | |
$5.1555$ | |
$6.1245$ |
Question 4 Explanation:
The correct choice is (B). To add decimals, vertically align the numbers so that the decimals are lined up. You can pad the shorter decimals by adding zeros to the end, and then add up the numbers:
$\begin{align} 1.7280& \\ 0.9975& \\ \underline{+\quad 2.4200}& \\ 5.1455& \end{align}$
$\begin{align} 1.7280& \\ 0.9975& \\ \underline{+\quad 2.4200}& \\ 5.1455& \end{align}$
Question 5 |
Rose correctly answered 70% of the spelling bee questions. If there were 220 questions total, how many did she answer incorrectly?
$66$ | |
$82$ | |
$129$ | |
$154$ |
Question 5 Explanation:
The correct choice is (A). 70% of 220 translates to:
$\dfrac{70}{100} \ast 220 = 154$
(We can estimate this value: 70% of 100 = 70 and 70% of 10 = 7, so 70% of 220 must equal 70 + 70 + 7 + 7 = 154.)
The question asks how many she answered incorrectly, so from the total number of questions, we must subtract the number of questions she answered correctly:
$220 − 154 = 66$
$\dfrac{70}{100} \ast 220 = 154$
(We can estimate this value: 70% of 100 = 70 and 70% of 10 = 7, so 70% of 220 must equal 70 + 70 + 7 + 7 = 154.)
The question asks how many she answered incorrectly, so from the total number of questions, we must subtract the number of questions she answered correctly:
$220 − 154 = 66$
Question 6 |
Multiply:
$8.32 × 3.2 =$$26.624$ | |
$266.24$ | |
$41.6$ | |
$0.416$ |
Question 6 Explanation:
The correct choice is (A). To multiply decimals, line up the numbers on the right (do not align the decimal points). Then starting on the right, multiply each digit of the top number by each digit of the bottom number. Then add the products:
$\begin{align} 8.32& \\ \underline{×\quad 3.2}& \\ 1664 \\ \underline{+\quad 2496\phantom{0}}& \\ 26.624& \end{align}$
Once you add the products, you must place the decimal point correctly. There are two decimal places in 8.32 and one decimal place in 3.2. Adding these decimal places together gives 3. Starting at the right of our answer move 3 places to the left and put the decimal point there.
$\begin{align} 8.32& \\ \underline{×\quad 3.2}& \\ 1664 \\ \underline{+\quad 2496\phantom{0}}& \\ 26.624& \end{align}$
Once you add the products, you must place the decimal point correctly. There are two decimal places in 8.32 and one decimal place in 3.2. Adding these decimal places together gives 3. Starting at the right of our answer move 3 places to the left and put the decimal point there.
Question 7 |
$3\dfrac{2}{5} + 1\dfrac{4}{7} =~?$
$\dfrac{145}{34}$ | |
$\dfrac{174}{35}$ | |
$\dfrac{168}{35}$ | |
$\dfrac{159}{34}$ |
Question 7 Explanation:
The correct choice is (B). To add mixed number fractions, first convert them to improper fractions, then find a common denominator and add or subtract the numerators, placing them over the common denominator. Reduce the final fraction if necessary.
To convert a mixed fraction to an improper fraction, multiply the whole number with the denominator, add this to the numerator, and place the resulting value above the original denominator.
$3\dfrac{2}{5} = \dfrac{17}{5}$
$1\dfrac{4}{7} = \dfrac{11}{7}$
Now find the lowest common denominator between 5 and 7. Since they are both prime numbers, their lowest common denominator is their product, 35. We can rewrite both fractions:
$\dfrac{17}{5} = \dfrac{119}{35}$
$\dfrac{11}{7} = \dfrac{55}{35}$
Now that the denominators are the same, we can add the numerators.:
$119 + 55 = 174$
To convert a mixed fraction to an improper fraction, multiply the whole number with the denominator, add this to the numerator, and place the resulting value above the original denominator.
$3\dfrac{2}{5} = \dfrac{17}{5}$
$1\dfrac{4}{7} = \dfrac{11}{7}$
Now find the lowest common denominator between 5 and 7. Since they are both prime numbers, their lowest common denominator is their product, 35. We can rewrite both fractions:
$\dfrac{17}{5} = \dfrac{119}{35}$
$\dfrac{11}{7} = \dfrac{55}{35}$
Now that the denominators are the same, we can add the numerators.:
$119 + 55 = 174$
Question 8 |
If $n$ is a positive integer divisible by $7$, and if $n < 70$, what is the greatest possible value of $n$?
$49$ | |
$56$ | |
$63$ | |
$69$ |
Question 8 Explanation:
The correct choice is (C). If you know one multiple of a number, you can find the other multiples by adding and subtracting that number. The number 70 is divisible by 7. The greatest multiple that is less than 70 will be 70 − 7 = 63.
Question 9 |
What is the value of $x$ in the triangle below?
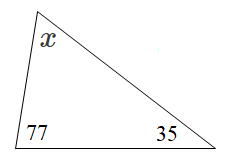
$35$ | |
$48$ | |
$55$ | |
$68$ |
Question 9 Explanation:
The correct choice is (D). The sum of all 3 interior angles in a triangle is 180°:
$x + 77 + 35 = 180$
$x + 112 = 180$
$x = 180 − 112$
$x = 68$
$x + 77 + 35 = 180$
$x + 112 = 180$
$x = 180 − 112$
$x = 68$
Question 10 |
Sam wants to cover his garden patio with brick tiles. His patio measures 15 feet by 20 feet. Each tile is 1 foot × 1 foot and costs \$2. How much money will Sam spend if he buys exactly enough tiles to cover his patio?
$\$250$ | |
$\$300$ | |
$\$450$ | |
$\$600$ |
Question 10 Explanation:
The correct choice is (D). First calculate the area of the patio:
$\text{Area} = 15 × 20$ $ = 300 \text{ ft}^2$
Since each tile is 1 square foot (1 × 1), it will take 300 tiles to cover the patio. Each tile costs \$2:
$300 × \$2 = \$600$
$\text{Area} = 15 × 20$ $ = 300 \text{ ft}^2$
Since each tile is 1 square foot (1 × 1), it will take 300 tiles to cover the patio. Each tile costs \$2:
$300 × \$2 = \$600$
Question 11 |
The fraction below is approximately equal to what value?
$\dfrac{1795}{95}$$15$ | |
$18$ | |
$20$ | |
$25$ |
Question 11 Explanation:
The correct choice is (B). Begin by rounding the numerator and denominator to numbers that are easier to work with: 1795 is about 1800 and 95 is about 100, so the expression becomes 1800 ÷ 100, which simplifies to 18.
Question 12 |
$\dfrac{3}{7} × \dfrac{15}{12} =~?$
$\dfrac{3}{21}$ | |
$\dfrac{15}{84}$ | |
$\dfrac{36}{77}$ | |
$\dfrac{15}{28}$ |
Question 12 Explanation:
The correct choice is (D). To multiply fractions, simply multiply the numerators to get the new numerator, and multiply the denominators get the new denominator.
$\dfrac{3}{7} × \dfrac{15}{12} = \dfrac{3 × 15}{7 × 12}$
Cancelling out a 3 in the top and bottom, we get:
$\dfrac{1 × 15}{7 × 4} = \dfrac{15}{28}$
$\dfrac{3}{7} × \dfrac{15}{12} = \dfrac{3 × 15}{7 × 12}$
Cancelling out a 3 in the top and bottom, we get:
$\dfrac{1 × 15}{7 × 4} = \dfrac{15}{28}$
Question 13 |
Divide:
$12 ÷ 50 =$ ?$0.24$ | |
$4.2$ | |
$2.4$ | |
$0.024$ |
Question 13 Explanation:
The correct choice is (A). This problem can be solved with long division. Since 50 can't even be divided into 12 one time, we know our answer will be less than 1. Add a decimal after the 12 and place a 0 to the right of it (12 and 12.0 are the same number). Also place a decimal above the line. Now, 50 can go into 120 twice, so place a 2 above the line and proceed with your long division:
$\require{enclose} \begin{array}{rll} \phantom{000} 0.24 & \\[-3pt] 50 \enclose{longdiv}{12.0\phantom{0}}\kern-.2ex \\[-3pt] -\underline{10\phantom{.}0\phantom{0}} \\ 200\phantom{.} \\ -\underline{ 200\phantom{.}} \\ 0\phantom{.} \\ \end{array}$
We can double check our answer by multiplying:
$0.24 × 50 = 12$
$\require{enclose} \begin{array}{rll} \phantom{000} 0.24 & \\[-3pt] 50 \enclose{longdiv}{12.0\phantom{0}}\kern-.2ex \\[-3pt] -\underline{10\phantom{.}0\phantom{0}} \\ 200\phantom{.} \\ -\underline{ 200\phantom{.}} \\ 0\phantom{.} \\ \end{array}$
We can double check our answer by multiplying:
$0.24 × 50 = 12$
Question 14 |
Karen, James, Frank, and Dan were left an inheritance by their late grandfather. If Karen receives one-eighth of the inheritance, James receives one quarter of the inheritance, Frank receives three-eighths of the inheritance, and Dan receives the remainder, what fraction of the inheritance does Dan receive?
$\dfrac{1}{4}$ | |
$\dfrac{5}{16}$ | |
$\dfrac{3}{8}$ | |
$\dfrac{3}{4}$ |
Question 14 Explanation:
The correct choice is (A). We can add up the fractions received by Karen, James, and Frank as follows:
$\dfrac{1}{8} + \dfrac{1}{4} + \dfrac{3}{8}$
$= \dfrac{1}{8} + \dfrac{2}{8} + \dfrac{3}{8}$
$= \dfrac{6}{8} = \dfrac{3}{4}$
We can find the fraction Dan receives by subtracting the sum of the other three fractions from one, since all the fractions must add up to one. Dan will receive:
$1 − \dfrac{3}{4} = \dfrac{1}{4}$
$\dfrac{1}{8} + \dfrac{1}{4} + \dfrac{3}{8}$
$= \dfrac{1}{8} + \dfrac{2}{8} + \dfrac{3}{8}$
$= \dfrac{6}{8} = \dfrac{3}{4}$
We can find the fraction Dan receives by subtracting the sum of the other three fractions from one, since all the fractions must add up to one. Dan will receive:
$1 − \dfrac{3}{4} = \dfrac{1}{4}$
Question 15 |
44 is 80% of what number?
$51$ | |
$53$ | |
$55$ | |
$57$ |
Question 15 Explanation:
The correct choice is (C). Let’s make up a variable for the correct answer. We can translate the question to read: 44 is 80% of $x$. In math, “is” means equals, and “of” means multiplication. Therefore, we can further translate this question into a simple equation:
$44 = 0.8x$
To solve, divide both sides by the decimal:
$\dfrac{44}{0.8} = x$
$x = 55$
$44 = 0.8x$
To solve, divide both sides by the decimal:
$\dfrac{44}{0.8} = x$
$x = 55$
Question 16 |
Which of the following numbers is the greatest?
$\dfrac{2}{3} \quad 0.6 \quad \dfrac{13}{22} \quad 0.08$$\dfrac{2}{3}$ | |
$0.6$ | |
$\dfrac{13}{22}$ | |
$0.08$ |
Question 16 Explanation:
The correct choice is (A). To determine which value is the greatest, convert the fractions to decimals and compare each value:
$\dfrac{2}{3} = 2 \div 3 = 0.66$
$\dfrac{13}{22} = 13 \div 2 = 0.59$
So the numbers from largest to smallest are:
$0.66 \quad 0.6 \quad 0.59 \quad 0.08$
$\dfrac{2}{3} = 2 \div 3 = 0.66$
$\dfrac{13}{22} = 13 \div 2 = 0.59$
So the numbers from largest to smallest are:
$0.66 \quad 0.6 \quad 0.59 \quad 0.08$
Question 17 |
Enrique is driving to Texas. He travels at 70 kilometers per hour for 2 hours, and 63 kilometers per hour for 5 hours. Over the 7 hour time period what was Enrique's average speed?
$64 \text{ km/h}$ | |
$65 \text{ km/h}$ | |
$66 \text{ km/h}$ | |
$67 \text{ km/h}$ |
Question 17 Explanation:
The correct choice is (B). Use this formula to find his average speed:
$\text{Avg Speed} = \dfrac{\text{Total Distance}}{\text{Total Time}}$
$\text{Total Distance:}$
$= 2(70) + 5(63)$
$= 140 + 315$
$= 455 \text{ km}$
$\text{Total Time:}$
$= 7 \text{ hours}$
$\text{Average Speed:}$
$= 455 ÷ 7$
$= 65 \text{ km/h}$
$\text{Avg Speed} = \dfrac{\text{Total Distance}}{\text{Total Time}}$
$\text{Total Distance:}$
$= 2(70) + 5(63)$
$= 140 + 315$
$= 455 \text{ km}$
$\text{Total Time:}$
$= 7 \text{ hours}$
$\text{Average Speed:}$
$= 455 ÷ 7$
$= 65 \text{ km/h}$
Question 18 |
What is the remainder when 814 is divided by 7?
$0$ | |
$1$ | |
$2$ | |
$3$ |
Question 18 Explanation:
The correct choice is (C). Use long division to solve this problem. As seen below, 814 divided by 7 equals 116 R 2:
$\require{enclose} \begin{array}{rll} 116 & \\[-3pt] 7 \enclose{longdiv}{814}\kern-.2ex \\[-3pt] -\underline{7\phantom{00}} \\ 11\phantom{0} \\ -\underline{ 7\phantom{0}} \\ \phantom{0}44 \\ -\underline{42} \\ \phantom{0}2 \\ \end{array}$
$\require{enclose} \begin{array}{rll} 116 & \\[-3pt] 7 \enclose{longdiv}{814}\kern-.2ex \\[-3pt] -\underline{7\phantom{00}} \\ 11\phantom{0} \\ -\underline{ 7\phantom{0}} \\ \phantom{0}44 \\ -\underline{42} \\ \phantom{0}2 \\ \end{array}$
Question 19 |
What is 14% of 75?
$10.5$ | |
$12.5$ | |
$14.0$ | |
$15.5$ |
Question 19 Explanation:
The correct choice is (A). The word “of” in math means multiplication, so “14% of 75” is equal to 0.14 × 75. You can find the correct answer of 10.5 by doing the multiplication or by estimating.
To estimate, we know that 10% of 75 = 7.5. And 4% of 75 would be a little less than half of 7.5 (let’s estimate 3.5), so we can approximate 14% of 75 as something close to 7.5 + 3.5 = 11.
To estimate, we know that 10% of 75 = 7.5. And 4% of 75 would be a little less than half of 7.5 (let’s estimate 3.5), so we can approximate 14% of 75 as something close to 7.5 + 3.5 = 11.
Question 20 |
Subtract:
$101.709 − 0.09 =$
$101.619$ | |
$110.799$ | |
$101.7$ | |
$100.809$ |
Question 20 Explanation:
The correct choice is (A). Use subtraction with regrouping to solve. Be sure to vertically align the numbers so that the decimals are lined up. You can pad the shorter decimal by adding a zero to the end:
$\begin{align} 101.709& \\ \underline{-\quad 0.090}& \\ 101.619& \end{align}$
$\begin{align} 101.709& \\ \underline{-\quad 0.090}& \\ 101.619& \end{align}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
