ACCUPLACER QAS Test Prep
If you are serious about getting a great score on your Accuplacer QAS test, try out our recommended Accuplacer QAS Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Solve for $x$:
$6(x − 3) = 4x + 4$$2.2$ | |
$3.5$ | |
$11$ | |
$22$ |
Question 1 Explanation:
The correct answer is (D). Begin by distributing the 6 through the parentheses:
$6(x − 3) = 4x + 4$
$6x − 18 = 4x + 4$
Subtract 4$x$ from both sides to maintain the equality:
$2x − 18 = 4$
Add 18 to both sides and then divide the resulting equation by 2 to solve for $x$ as follows:
$2x = 22$
$x = 11$
$6(x − 3) = 4x + 4$
$6x − 18 = 4x + 4$
Subtract 4$x$ from both sides to maintain the equality:
$2x − 18 = 4$
Add 18 to both sides and then divide the resulting equation by 2 to solve for $x$ as follows:
$2x = 22$
$x = 11$
Question 2 |
A rectangle is cut in half to create two squares that each have an area of 25. What is the perimeter of the original rectangle?
$20$ | |
$25$ | |
$30$ | |
$35$ |
Question 2 Explanation:
The correct answer is (C). The formula to find the area of a square is $\text{side} \times \text{side}$. If each square has an area of $25$, then the dimensions of the rectangle are $5 \times 10$.
The perimeter is the sum of all the sides, and would therefore be $5 + 10 + 5 + 10 = 30$.
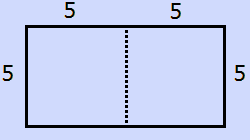
The perimeter is the sum of all the sides, and would therefore be $5 + 10 + 5 + 10 = 30$.

Question 3 |
Joe’s current age is five times Mary’s age ten years ago. If Mary is currently $m$ years old, what is Joe’s current age in terms of $m$?
$5m$ | |
$5m−10$ | |
$5m−50$ | |
$5m + (m −10)$ |
Question 3 Explanation:
The correct answer is (C). Mary’s age ten years ago is:
$m−10$
So Joe’s age is:
$5(m−10)$
$=5m−50$
$m−10$
So Joe’s age is:
$5(m−10)$
$=5m−50$
Question 4 |
Solve:
$\dfrac{2x}{5} + 5 < −5$$x>−20$ | |
$x>−10$ | |
$x<−20$ | |
$x<−25$ |
Question 4 Explanation:
The correct answer is (D). In order to isolate $x$, we must first subtract $5$ from both sides as follows:
$\dfrac{2x}{5}+5−5<−5−5$
$\dfrac{2x}{5}<−10$
Next, multiply both sides by $5$. Then divide both sides by $2$:
$2x<−50$
$x<−25$
$\dfrac{2x}{5}+5−5<−5−5$
$\dfrac{2x}{5}<−10$
Next, multiply both sides by $5$. Then divide both sides by $2$:
$2x<−50$
$x<−25$
Question 5 |
A vase contains 60 marbles, all of which are red or orange. If the ratio of red marbles to orange ones is 1:5, what is the total number of red marbles in the vase?
$8$ | |
$10$ | |
$12$ | |
$50$ |
Question 5 Explanation:
The correct answer is (B). We know that the ratio is 1:5. This means that for every six marbles one of them is red and five are orange. So $\frac{1}{6}$ of the marbles are red:
$\dfrac{1}{6} × 60 = 10$
$\dfrac{1}{6} × 60 = 10$
Question 6 |
Find the $x$-intercept of a line that has the following equation:
$2y=3x−6$$−2$ | |
$−1$ | |
$1$ | |
$2$ |
Question 6 Explanation:
The correct answer is (D). At the $x$-intercept, $y=0$. We can solve for the $x$-intercept by setting $y=0$ in the equation of the line:
$2y=3x−6$
$2(0)=3x−6$
$0=3x−6$
$3x=6$
$x=2$
$2y=3x−6$
$2(0)=3x−6$
$0=3x−6$
$3x=6$
$x=2$
Question 7 |
A bird traveled 72 miles in 6 hours flying at constant speed. At this rate, how many miles did the bird travel in 5 hours?
$12$ | |
$30$ | |
$60$ | |
$14.4$ |
Question 7 Explanation:
First calculate the rate that the bird is traveling at:
$\dfrac{72 \text{ miles}}{6 \text{ hours}}$ $ =12 \text{ miles per hour}$
The distance traveled in 5 hours will be:
$12 \text{ mph}∗5 \text{h}=60 \text{ miles}$
$\dfrac{72 \text{ miles}}{6 \text{ hours}}$ $ =12 \text{ miles per hour}$
The distance traveled in 5 hours will be:
$12 \text{ mph}∗5 \text{h}=60 \text{ miles}$
Question 8 |
$3^{−2}= \; ?$
$−9$ | |
$−6$ | |
$9$ | |
$\dfrac{1}{9}$ |
Question 8 Explanation:
The correct answer is (D). To evaluate a base raised to a negative exponent that is in the numerator, rewrite the expression with the base and exponent in the denominator, and rewrite the negative exponent as a positive exponent. In cases where the base raised to a negative exponent is in the denominator, rewrite the base and exponent in the numerator, and switch the sign of the exponent:
$a^{−n}=\dfrac{1}{a^n}$
$3^{−2}=\dfrac{1}{3^2}=\dfrac{1}{9}$
$a^{−n}=\dfrac{1}{a^n}$
$3^{−2}=\dfrac{1}{3^2}=\dfrac{1}{9}$
Question 9 |
There are 10 red marbles, 4 blue marbles, and 7 white marbles in a jar. One marble is chosen at random and then returned to the jar, and then a second marble is chosen at random. What is the probability that both of the marbles chosen are white?
$\dfrac{1}{3}$ | |
$\dfrac{1}{9}$ | |
$\dfrac{1}{6}$ | |
$\dfrac{2}{3}$ |
Question 9 Explanation:
The correct answer is (B). To calculate the probability that an event occurs, divide the number of possible successful events by the total number of events. In this case, a success is selecting a white marble, and the total number of events is the total number of marbles. Because the first selected marble is returned to the jar, the second selection does not depend on the first selection. To find the probability of consecutive independent events occurring, calculate the product of their probabilities.
The probability of selecting a white marble is:
$\dfrac{7 \text{ White Marbles}}{10+4+7 \text{ Total Marbles}}$
$=\dfrac{7}{21}=\dfrac{1}{3}$
To find the probability of selecting $2$ white marbles in row:
$\dfrac{1}{3}∗\dfrac{1}{3}=\dfrac{1}{9}$
The probability of selecting a white marble is:
$\dfrac{7 \text{ White Marbles}}{10+4+7 \text{ Total Marbles}}$
$=\dfrac{7}{21}=\dfrac{1}{3}$
To find the probability of selecting $2$ white marbles in row:
$\dfrac{1}{3}∗\dfrac{1}{3}=\dfrac{1}{9}$
Question 10 |
Jon likes to tip 20% at restaurants. To figure out the tip he should leave for a \$35 meal, he uses the following expression:
$0.20×35$ Which of the following expressions could Jon have also used?$\dfrac{35}{10} × 2$ | |
$35÷(1−0.20)−35$ | |
$\dfrac{35 × 100}{20}$ | |
$35÷4$ |
Question 10 Explanation:
The correct answer is (A). Dividing any number by 10 will give you the value of 10% of the original number.
So, $\frac{35}{10}$ gives us 3.50 which is 10% of 35.
To find 20% of 35, we simply double the value we found for 10%.
Thus, $\frac{35}{10}$ × 2 = 7.00 provides the correct result.
So, $\frac{35}{10}$ gives us 3.50 which is 10% of 35.
To find 20% of 35, we simply double the value we found for 10%.
Thus, $\frac{35}{10}$ × 2 = 7.00 provides the correct result.
Question 11 |
Which of the following expressions represents the square of the difference of $a$ and $b$?
$(a − b)^2$ | |
$\sqrt{a − b}$ | |
$a^2 − b^2$ | |
$\sqrt{a} − \sqrt{b}$ |
Question 11 Explanation:
The correct answer is (A). To find “the square of the difference” we need to first determine “the difference.”
The “difference of $a$ and $b$” can be expressed as: $a − b$
The “square of the difference” can be expressed as: $(a − b)^2$
$\sqrt{a − b} =$ The square root of the difference of $a$ and $b$
$a^2 − b^2 =$ The difference of the square of $a$ and the square of $b$
$\sqrt{a} − \sqrt{b} =$ The difference of the square root of $a$ and the square root of $b$
The “difference of $a$ and $b$” can be expressed as: $a − b$
The “square of the difference” can be expressed as: $(a − b)^2$
$\sqrt{a − b} =$ The square root of the difference of $a$ and $b$
$a^2 − b^2 =$ The difference of the square of $a$ and the square of $b$
$\sqrt{a} − \sqrt{b} =$ The difference of the square root of $a$ and the square root of $b$
Question 12 |
What is the number of cubic millimeters in 300 cubic centimeters?
(1 cubic centimeter = 1000 cubic millimeters)$3$ | |
$300{,}000$ | |
$0.3$ | |
$3{,}000{,}000$ |
Question 12 Explanation:
The correct answer is (B). We can solve this by setting up an equivalent proportion:
$\dfrac{1 \text{ cm}^3}{1000 \text{ mm}^3} = \dfrac{300 \text{ cm}^3}{x \text{ mm}^3}$
$(1)(x) = (1000)(300)$
$x = 300{,}000$
$\dfrac{1 \text{ cm}^3}{1000 \text{ mm}^3} = \dfrac{300 \text{ cm}^3}{x \text{ mm}^3}$
$(1)(x) = (1000)(300)$
$x = 300{,}000$
Question 13 |
Which of the following is the equation of the line that passes through the points $(0,8)$ and $(-4,0)$ on the $xy$-plane?
$y = 8x - 4$ | |
$y = 2x + 8$ | |
$y = - \dfrac{1}{2}x + 8$ | |
$y = -4x + 8$ |
Question 13 Explanation:
The correct answer is (B). All answers are expressed in slope-intercept form:
$y = mx + b$
$m = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{0 - 8}{-4 - 0}$ $ = \dfrac{-8}{-4} = 2$
The variable $b$ represents the $y$-intercept, which is actually given by the point $(0,8)$. When $x = 0, y = 8$. Thus, $b = 8$.
Substituting $m$ and $b$ into our equation yields:
$y = 2x + 8$
$y = mx + b$
$m = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{0 - 8}{-4 - 0}$ $ = \dfrac{-8}{-4} = 2$
The variable $b$ represents the $y$-intercept, which is actually given by the point $(0,8)$. When $x = 0, y = 8$. Thus, $b = 8$.
Substituting $m$ and $b$ into our equation yields:
$y = 2x + 8$
Question 14 |
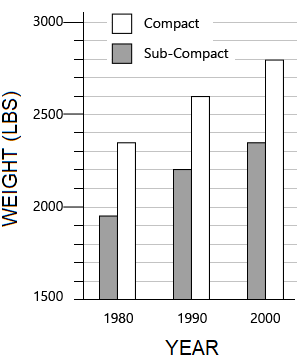
According to the graph which shows the weights of two different classes of cars (compact and sub-compact) for three different decades, for which of the following is the difference in weight greatest?
$\text{1990}$ $\text{Compact}$ $\text{versus}$ $\text{1980}$ $\text{Compact}$ | |
$\text{2000}$ $\text{Sub-Compact}$ $\text{versus}$ $\text{1980}$ $\text{Sub-Compact}$ | |
$\text{2000}$ $\text{Compact}$ $\text{versus}$ $\text{2000}$ $\text{Sub-Compact}$ | |
$\text{1980}$ $\text{Compact}$ $\text{versus}$ $\text{1980}$ $\text{Sub-Compact}$ |
Question 14 Explanation:
The correct answer is (C). Test each answer choice:
$A = 2600 − 2350 = 250$
$B = 2350 − 1950 = 400$
$C = 2800 − 2350 = 450$
$D = 2350 − 1950 = 400$
Answer (C) is the greatest difference.
$A = 2600 − 2350 = 250$
$B = 2350 − 1950 = 400$
$C = 2800 − 2350 = 450$
$D = 2350 − 1950 = 400$
Answer (C) is the greatest difference.
Question 15 |
$f(x) = \dfrac{2 + x}{3 + x}$
What is the minimum value of $x$ for which $f(x)$ will exceed 0.90?$7$ | |
$6$ | |
$9$ | |
$8$ |
Question 15 Explanation:
The correct answer is (D). We can express 0.90 as $\frac{90}{100}$ which can be simplified to $\frac{9}{10}$.
Using $\frac{9}{10}$ in place of 0.90 in the question gives:
What is the minimum value of $x$ for which $\frac{2 + x}{3 + x}$ exceeds $\frac{9}{10}$?
When $x = 7$ we have $\frac{2 + 7}{3 + 7} = \frac{9}{10}$. This does not exceed $\frac{9}{10}$.
When $x = 8$ we have $\frac{2 + 8}{3 + 8} = \frac{10}{11}$. This value of $x$ results in a fraction that exceeds $\frac{9}{10}$.
It may help to think of the size of $\frac{1}{11}$ versus $\frac{1}{10}$. Since $\frac{1}{11}$ is smaller than $\frac{1}{10}, \frac{10}{11}$ is greater than $\frac{9}{10}$ because the missing piece is smaller.
Using $\frac{9}{10}$ in place of 0.90 in the question gives:
What is the minimum value of $x$ for which $\frac{2 + x}{3 + x}$ exceeds $\frac{9}{10}$?
When $x = 7$ we have $\frac{2 + 7}{3 + 7} = \frac{9}{10}$. This does not exceed $\frac{9}{10}$.
When $x = 8$ we have $\frac{2 + 8}{3 + 8} = \frac{10}{11}$. This value of $x$ results in a fraction that exceeds $\frac{9}{10}$.
It may help to think of the size of $\frac{1}{11}$ versus $\frac{1}{10}$. Since $\frac{1}{11}$ is smaller than $\frac{1}{10}, \frac{10}{11}$ is greater than $\frac{9}{10}$ because the missing piece is smaller.
Question 16 |
Which of the following expressions is equivalent to $\left(\dfrac{x^3}{x^5}\right)^{−3}$?
$\dfrac{1}{x^5}$ | |
$\dfrac{1}{x^{24}}$ | |
$x^6$ | |
$x^5$ |
Question 16 Explanation:
The correct answer is (C). Begin by simplifying inside the parentheses. When dividing we subtract exponents.
$\left(\dfrac{x^3}{x^5}\right)^{−3} = \left(x^{3−5}\right)^{−3}$ $ = \left(x^{−2}\right)^{−3}$
When taking a power to a power we multiply exponents.
$\left(x^{−2}\right)^{−3} = x^{(−2)(−3)} = x^6$
$\left(\dfrac{x^3}{x^5}\right)^{−3} = \left(x^{3−5}\right)^{−3}$ $ = \left(x^{−2}\right)^{−3}$
When taking a power to a power we multiply exponents.
$\left(x^{−2}\right)^{−3} = x^{(−2)(−3)} = x^6$
Question 17 |
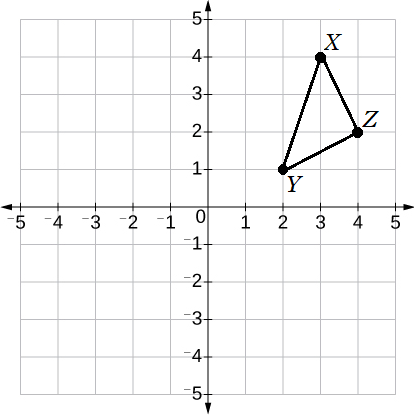
Triangle $XYZ$ lies in the $xy$-plane. The coordinates of vertex $X$ are $(3,4)$, the coordinates of vertex $Y$ are $(2,1)$, and the coordinates of vertex $Z$ are $(4,2)$.
If the triangle is rotated 270° clockwise to produce triangle $X'Y'Z'$, what will be the coordinates of vertex $X'$ which corresponds to vertex $X$ of triangle $XYZ$?$(−4,3)$ | |
$(3,−4)$ | |
$(−3,4)$ | |
$(4,−3)$ |
Question 17 Explanation:
The correct answer is (A). Rotating Triangle $XYZ$ 270° clockwise is the same as rotating it 90° counter-clockwise (ccw). We are interested in determining where vertex $x$ lands after being rotated 90° ccw.
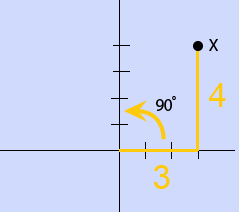
Position of $x'$ after $x$ has been rotated:
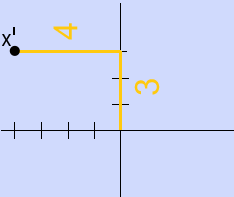
The coordinates of $x' = (−4, 3)$
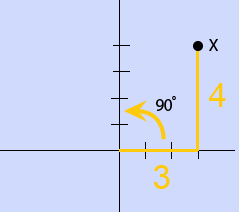
Position of $x'$ after $x$ has been rotated:

The coordinates of $x' = (−4, 3)$
Question 18 |
Mr. Red, Mr. Green, and Mr. Blue each has a billiard ball whose color matches his last name. Each places his ball into the same bag. The balls are mixed, and then each of the men removes one ball from the bag without looking. What is the probability that only one man draws his original ball?
$\dfrac{1}{2}$ | |
$\dfrac{1}{3}$ | |
$\dfrac{2}{3}$ | |
$\dfrac{1}{6}$ |
Question 18 Explanation:
The correct answer is (A). When the number of possibilities is low we can list all possible outcomes to determine the answer.
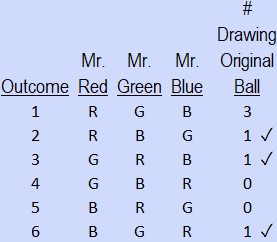
In 3 of the 6 outcomes, only one man draws his original ball.
Thus, the probability is $\frac{3}{6}$ or $\frac{1}{2}$.

In 3 of the 6 outcomes, only one man draws his original ball.
Thus, the probability is $\frac{3}{6}$ or $\frac{1}{2}$.
Question 19 |
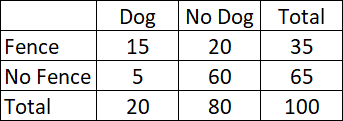
The table above shows the results of a 100-person survey. Each person was asked if they owned a dog and if their yard was fenced-in. Given that the person's yard is fenced, what is the probability that they own a dog?
$\dfrac{3}{7}$ | |
$\dfrac{1}{5}$ | |
$\dfrac{3}{4}$ | |
$\dfrac{3}{20}$ |
Question 19 Explanation:
The correct answer is (A).
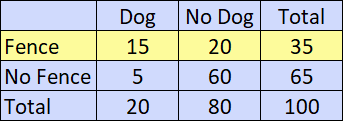
"Given that the person's yard is fenced" means we are only looking at the first row (highlighted).
Looking only at this first row, the probability that the person owns a dog is:
$\dfrac{15}{35} = \dfrac{3}{7}$

"Given that the person's yard is fenced" means we are only looking at the first row (highlighted).
Looking only at this first row, the probability that the person owns a dog is:
$\dfrac{15}{35} = \dfrac{3}{7}$
Question 20 |
A laser cutting machine has an initial value of \$250,000. Its value is depreciating (going down) by \$15,000 each year. Let $v(t)$ be the value in dollars of the laser cutter as a function of time, $t$, in years. Which of the following equations properly models this situation?
$v(t) = 250{,}000t − 15{,}000$ | |
$v(t) = −250{,}000t − 15{,}000$ | |
$v(t) = −15{,}000t + 250{,}000$ | |
$v(t) = 15{,}000 − 250{,}000t$ |
Question 20 Explanation:
The correct answer is (C). The slope-intercept form of a linear equation is:
$y = mx + b$
In this particular problem the dependent variable is $v$ and the independent variable is $t$, so our equation will be of the form:
$v(t) = mt + b$
The value is going down by $\$15{,}000$ per year. This gives us a slope (rate of change) of: $m = −15{,}000$
The initial value (when $t = 0$) is $\$250{,}000$. This means our $y$-intercept (actually "$v$-incercept") will be: $b = 250{,}000$
The equation of our line is: $v = −15{,}000t + 250{,}000$
$y = mx + b$
In this particular problem the dependent variable is $v$ and the independent variable is $t$, so our equation will be of the form:
$v(t) = mt + b$
The value is going down by $\$15{,}000$ per year. This gives us a slope (rate of change) of: $m = −15{,}000$
The initial value (when $t = 0$) is $\$250{,}000$. This means our $y$-intercept (actually "$v$-incercept") will be: $b = 250{,}000$
The equation of our line is: $v = −15{,}000t + 250{,}000$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
